《现代物理有机化学》笔记：有机电子材料

17.1.1 无限$\pi$体系：特别的聚乙炔

首先绘制出“聚乙炔”的能级图：

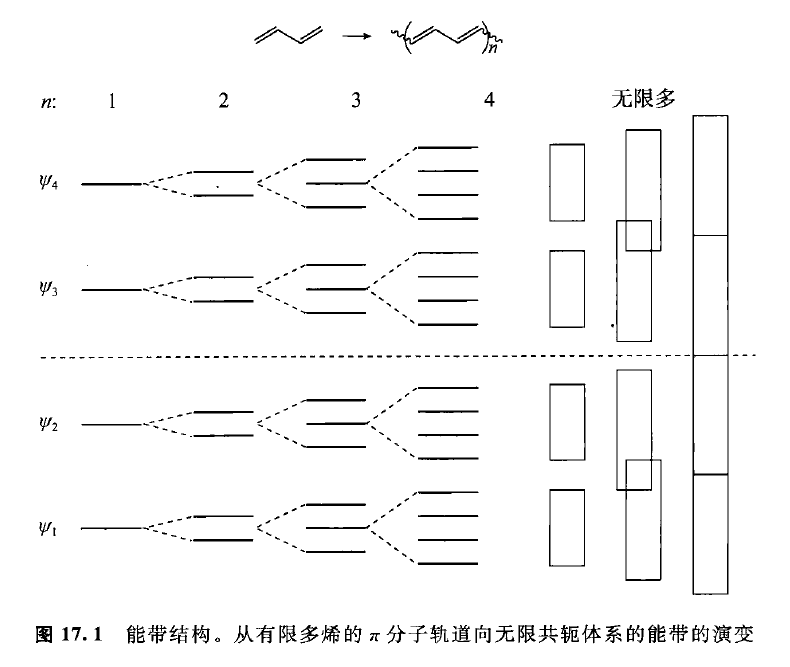
而我们处理的策略就是将线性体系以环多烯的方式处理，因为它们的电子结构差不多，它们的能级满足以下关系：$\epsilon =\alpha +2\cos(\frac{2\pi i}{ N})\times \beta$，其中$i$为轨道节点数目，$N$为原子总数目。例如，我们分析环戊二烯自由基（$N=5$）：

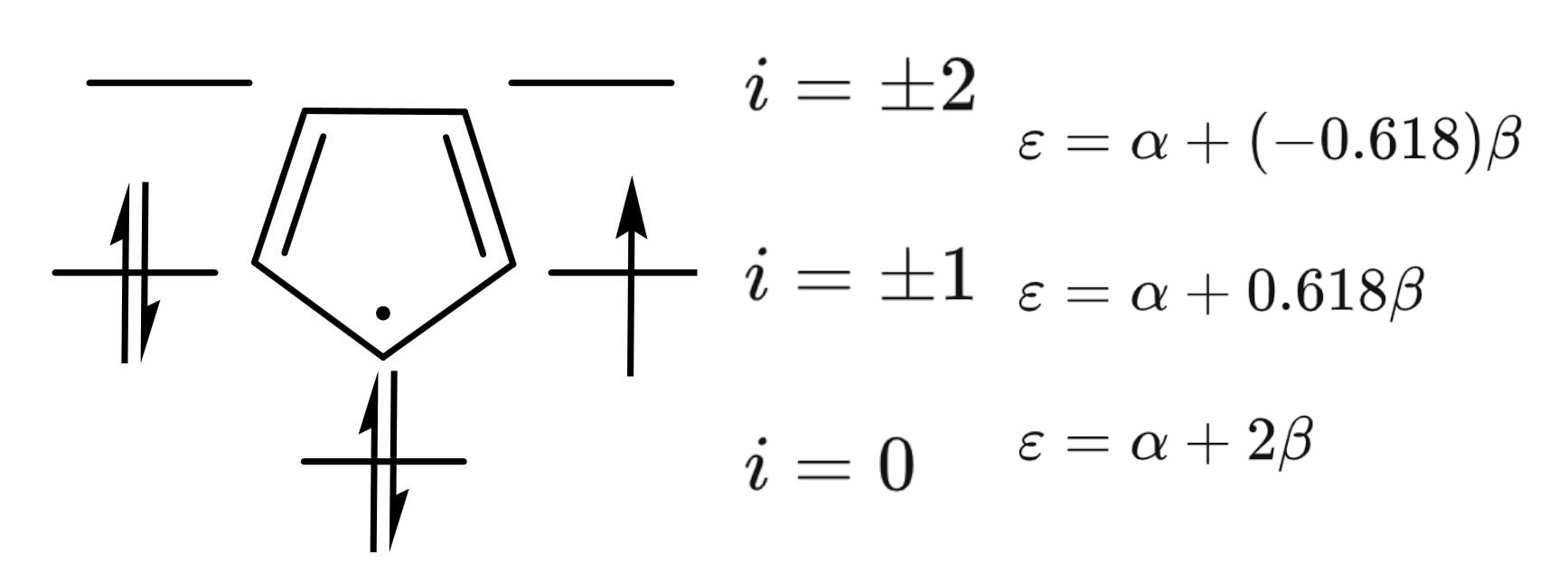
其中，$i=\pm 2$时的轨道是反键轨道，其余的是成键轨道。那么，当$N\to + \infty $时，我们就可以作出$\epsilon$关于$i$变化的图像：

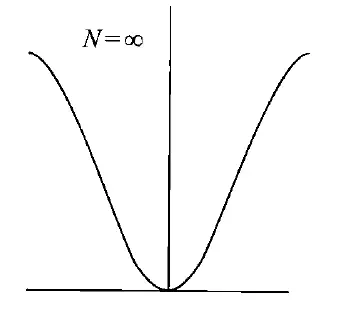
可以看出，它类似于一个正弦曲线，最小值为$\alpha+2\beta$，最大值为$\alpha-2\beta$。

倘若我们将固体化学的概念引入这里，比如“晶胞”，即“重复单元”，然而，无限$\pi$体系中的所有$\mathrm{CH} $都是等价的，即聚乙炔的晶胞都是一个$\mathrm{CH} $，那么我们定义$a$为一个$\mathrm{CH} $的大小，和$k$($k=\frac{2\pi i}{Na} $)由于$-\frac{N}{a} \le i\le +\frac{N}{a}$，那么$-\frac{\pi}{a} \le k\le +\frac{\pi}{a}$，将$k$代入$\epsilon$的定义式中，得到$\epsilon=\alpha+\cos( ka )\times\beta$，则可以作出相应的图像：

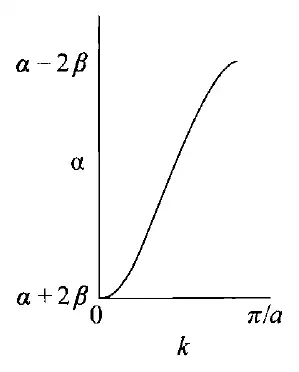
代表着能带内“相”的关系，代表着“相空间”，即$\pi$轨道相位组合的方式。$k=0$时，所有单体的相位相同，$k=\frac{\pi}{a} $时，所有单体的相位相反。

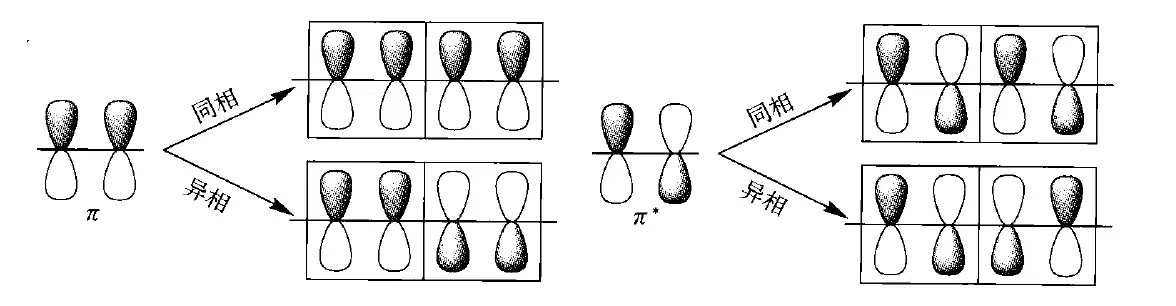
$k=0$时，所有相位相同，此时能量应最低，为$\alpha+2\beta$； 时，所有单体的相位相反，能量最高，为$\alpha-2\beta$；而π轨道（如上图中左下侧）异相组合时，能量应呈现非键轨道特性，为$\alpha$。（注意：这里原书认为单体，即重复单元为两个$\mathrm{CH} $，那么相应地，单体长度也会扩大两倍，变成 $a'$，$a'=2a$）

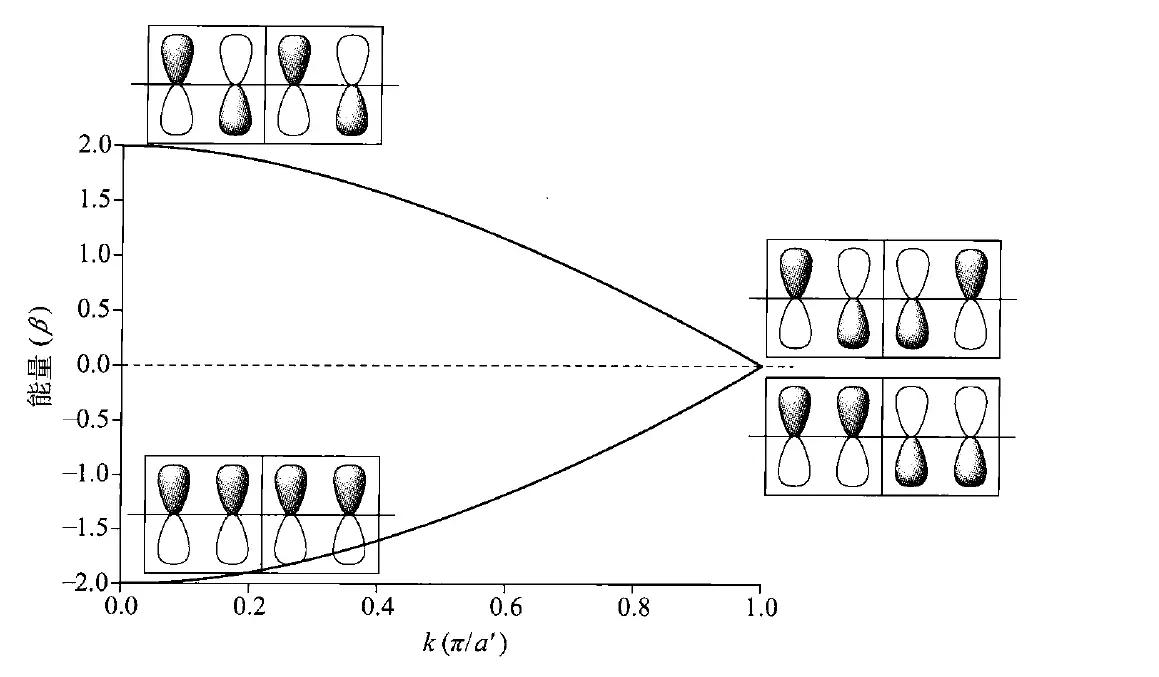
不过，不管怎么取“晶胞”，分子的电子结构都不会改变，那么理论上，聚乙炔的π轨道应当全满，$\pi^{\star}$ 轨道应当全空，其Fermi能级（$E_{F}$，和HOMO是一个意思）就在中间，能量为$\alpha$ 。但在这个模型中，能带（$\pi$ 和 $\pi^{\star}$ 轨道组成的）之间的能级差（$E_{g}$，能隙）应该为 ，所以，聚乙炔就应该是一种有机金属导体了！可惜事实真的如此吗？

更何况，真实的材料可不会是一维的，所以以上分析还是有点瑕疵。这也是Hückel理论的一个缺陷。

---

17.1.2 Peierls形变

我们发现，在Hückel理论中，聚乙炔的能隙等于$0$，而环丁二烯也是一个类似的体系：

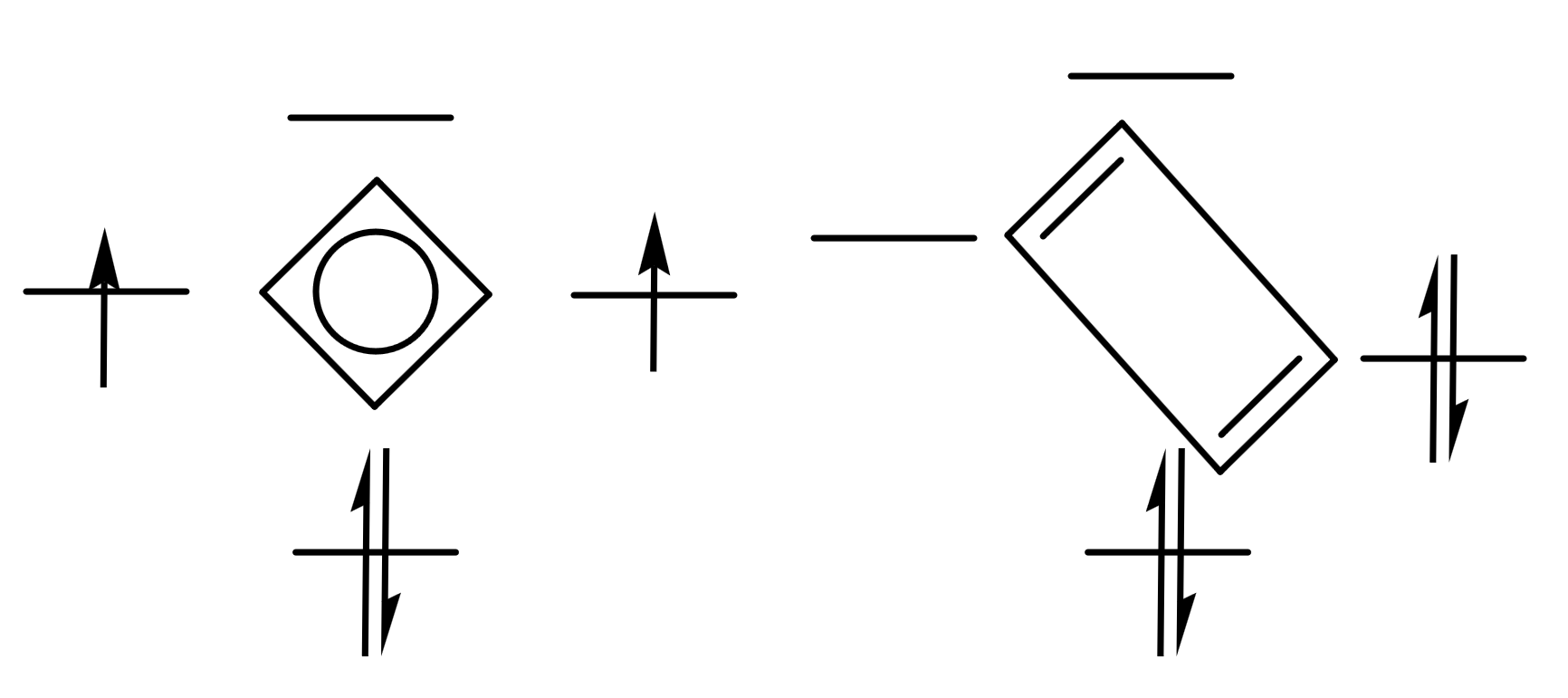
如果不谈反芳香性等等因素的话，那环丁二烯本来应该是正方形的，这没什么问题。但是它实际上处于一个矩形的构型（长键长$1.54\mathrm{Å}$，短键长$1.37\mathrm{Å}$），这就导致HOMO和LUMO裂分，从而变得更稳定——矩形的构型能量比正方形低$5-10\mathrm{kcal/mol}$——这也可以被称作是“伪Jahn-Teller效应”。因此，环丁二烯的基态应该是单重态（上图右），而非三重态（上图左），正方形的构型其实算是两种矩形构型交替变化的一个过渡态罢了。

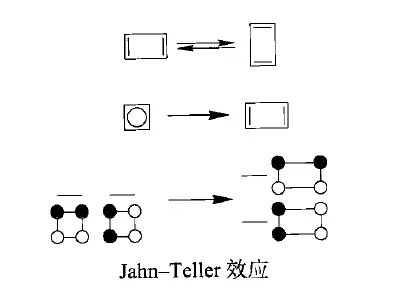
类似的效应在聚乙炔中也出现了，按照我们的预期，聚乙炔的C-C键应该都是等长的——可事实却不是这样，它的键长发生了形变，变成了长短交替的结构。几何形变让它出现了能隙，$E_{g}=1.5\mathrm{eV}$，所以实际上，聚乙炔是一种半导体，这种形变叫做Peierls形变。

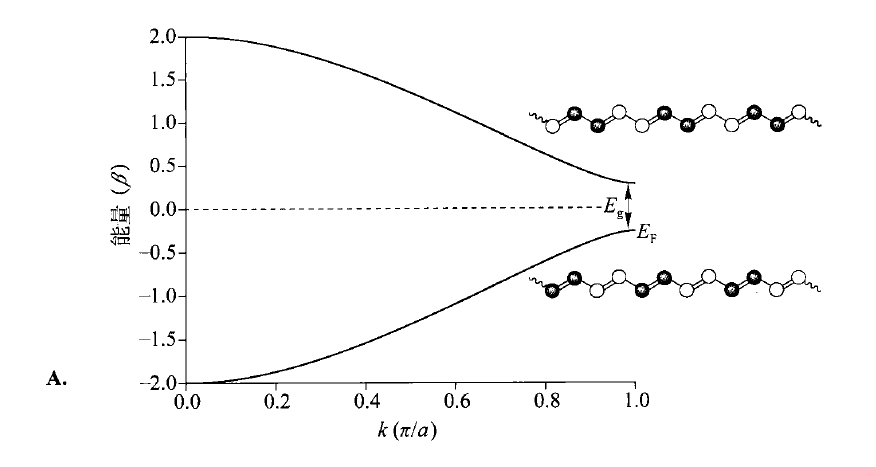
此时，聚乙炔的HOMO（也就是$E_{F}$）是低于$\alpha$的，确实是稳定化了。其实在多数中性、闭壳的$\pi$体系中，这种长短键交替的现象是比较常见的。苯算是一个特例，由于强$\sigma$键的束缚，它的键长的确是均一的。

---

17.1.3 掺杂

在$\pi$体系共轭聚合物中，聚乙炔等等只能算是半导体，而绝缘体更是普遍的情况。所以，为了改善它们的导电性，掺杂是一个很好的办法。例如把聚合物置于氧化剂（如$\mathrm{AsF_{5}}$，$\mathrm{I_{2}}$）氛围中，让其失去电子，引入正电荷，进行p型掺杂；或是用还原剂（如金属钠，萘-钠）处理进行n型掺杂。那么我们先讨论p型掺杂。

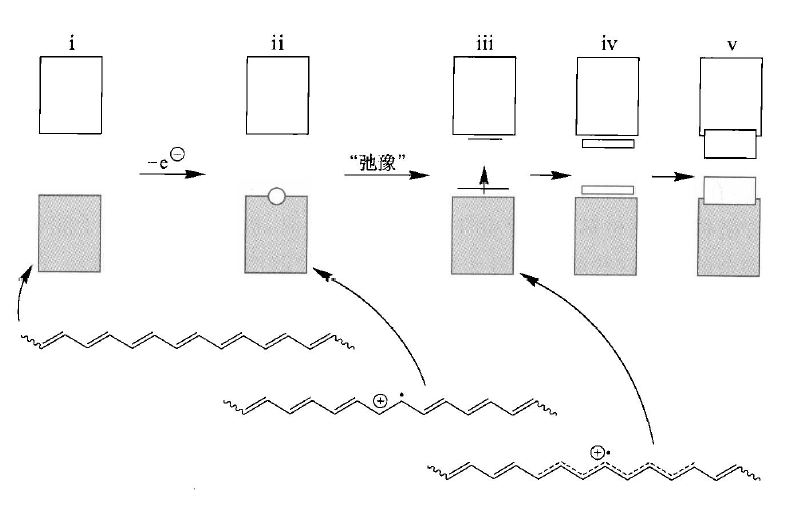
进行n型掺杂，引入正电荷或自由基后会产生一个部分离域的正离子，为什么是部分离域呢？

• 我们知道，烯丙基自由基比乙基自由基稳定，是因为它有离域体系，然而随着离域体系越来越大，自由基应该是更稳定的，随着碳原子数的增加，例如戊二烯基自由基，肯定是比烯丙基自由基稳定的，但是它们之间能量的差值会越来越小，到最后，离域提供的稳定化能只能说是微乎其微，不足挂齿了。（可能可以用共轭饱和理论来解释）

• 另外，由于Peierls形变为聚合物提供了稳定化能，但是掺和进来的正离子或自由基打乱了这个节奏，离域的能量不足以补偿打乱Peierls形变抬升的能量。

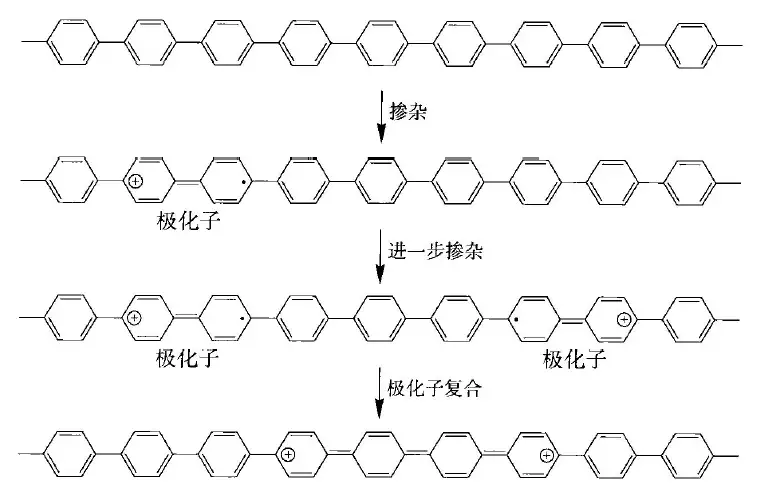
随着掺杂得越来越多，产生的部分离域的电荷和自由基（称作“极化子”）也会变得越来越多，使得电导率上升。

这样掺杂的一个结果，就是能够形成“中间能隙束缚态”，代表着电子的缺失，也可以看作空轨道的引入，单占轨道从价带中独立出去。它的另一种解释是极化子的形成消除了Peierls形变。并且，新轨道的产生使得光学跃迁成为了可能，让产生的聚合物带上了颜色。

重度掺杂也会导致“双极化子”的形成，它可能是两个极化子复合而成的。如果极化子是自由基，则它们会复合成新键；若是电荷，库仑斥力不应该会阻碍它们的复合吗？在气相中的确是这样的，但在固相中，材料的介电系数更大，减小了库仑斥力，并且引入的阴离子，如 $\mathrm{As_{2}F_{11}^{-}}$、$\mathrm{I_{3}^{-}}$等，扩散能力较强，屏蔽了其电荷，促使双极化子产生。

与金属导体不同，这些聚合物的电导率（$\sigma$，电阻率$\rho$的倒数）常常与温度反相关，这是因为极化子的移动会导致碳骨架（它们的键长、键角等）轻微地改变，这需要一定的热活化能。金属在低温时，干扰晶格中自由电子运动的振动会减少。综上，电导率与温度的关系也是判定是否为金属导体的一大标准。

以上是对于p型掺杂半导体的论述，同理，n型掺杂也是差不多的。

---

致谢

特别感谢@lesscho 对本文的斧正，感恩捏！

---

原文发表在知乎。