数据结构课程板子合集&笔记

关于数据结构

数据结构研究组织数据（结构化信息）的方法，以支持有效——满足时空限制的处理。

数据

数据是计算机程序要处理的“原料” 是所有被计算机识别、存储和加工处理的符号的总称。

数据元素是组成数据的基本单位，也称数据成分、元素、结点等。数据可理解成数据元素的集合。数据元素可大可小，在程序中通常把一个数据元素作为一个整体来考虑和处理。

数据元素可由若干数据项组成。数据项也称为域、字段等。

数据结构

数据结构由三部分组成：

  • 数据的逻辑结构：数据元素和它们之间的逻辑关系。

  • 数据的存储结构：逻辑结构到存储空间的映射。

    • 顺序存储结构
    • 链接存储结构
    • 索引存储结构
    • 散列存储结构

  • 运算（操作）：CURD、排序

算法

算法是有穷规则的集合，规定了解决某一特定
类型问题的运算序列。

通常，一个算法有5个重要特性（Knuth）：

  1. 有限性：算法必须在执行有限步后结束；
  2. 确定性：算法描述必须无歧义，通常结果确定；
  3. 可行性：算法中的运算必须是可行的；
  4. 输入：一个算法有零个或多个输入；
  5. 输出：一个算法有一个或多个输出；

线性表-栈-队列

概念辨析

特性线性表堆栈队列链表
逻辑结构一对一的有序集合特殊的线性表（LIFO）特殊的线性表（FIFO）物理存储结构
操作限制无特殊限制只能在栈顶操作队尾插入，队头删除无特殊限制
实现方式顺序表、链表顺序栈、链式栈顺序队列、链式队列单向链表、双向链表、循环链表
访问方式支持随机访问（顺序表）不支持随机访问不支持随机访问不支持随机访问
典型应用通用数据存储函数调用栈、表达式求值任务调度、缓冲区管理动态数据存储

字符串

模式匹配

朴素的模式匹配，复杂度为O(mn)O(mn)

利用KMP算法的思想，需要实现前缀函数/失败函数：

f(j)={k,k 为满足 p0p1…pk=pj−kpj−k+1…pj 的最大值，且 0≤k<j−1,其他情况f(j) = \begin{cases} k, & \text{\( k \) 为满足 } p_0 p_1 \dots p_k = p_{j-k} p_{j-k+1} \dots p_j \text{ 的最大值，且 } 0 \leq k < j \\ -1, & \text{其他情况} \end{cases}

KMP算法实现1

前缀函数

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> pi(string&s)
{
    int n=s.length();
    vector<int>pi(n);
    for(int i=1;i<n;i++)
    {
        int j=pi[i-1];
        while(j>0&&s[i]!=s[j]) j=pi[j-1];
        if(s[i]==s[j]) j++;
        pi[i]=j;
    }
    return pi;
}

时间复杂度O(n)O(n)。

查找子串

1
2
3
4
5
6
7
8
9
10
11
12
vector<int> KMP(string&text,string&pattern) 
{
    string cur=pattern+'#'+text;
    int sz1=text.size(),sz2=pattern.size();
    vector<int> v;
    vector<int> lps=pi(cur);
    for(int i=sz2+1;i<=sz1+sz2;i++)
    {
        if (lps[i]==sz2) v.push_back(i-2*sz2);
    }
    return v;
}

KMP算法实现2

next数组

next[j]: j前字符串的最长公共前缀后缀的长度。

1
2
3
4
5
6
7
8
9
10
11
12
void cal_next(char p[]) {
    int i = 0, j = -1, m = strlen(p); // i 是后缀指针，j 是前缀指针
    next[0] = -1; // 初始化 next[0] 为 -1
    while (i < m - 1) {
        if (j == -1 || p[i] == p[j]) {
            i++, j++;
            next[i] = j; // 更新 next[i]
        } else {
            j = next[j]; // 回溯 j
        }
    }
}

查找子串

1
2
3
4
5
6
7
8
int kmp(char s[],char p[]) {
    int i=0,j=0,n=strlen(s),m=strlen(p);
    if (n < 1 || m < 1 || n < m) return -1;
    while(i < n && j < m)
        if(j==-1 || s[i]==p[j]) i++,j++;
        else j = next[j] ;
    return j==m ? i-j : -1;
}

总结和注意事项

next 数组的定义

  • next[i] 表示模式串 p 的前缀 p[0...i-1] 的最长公共前后缀的长度。
  • next[0] 固定为 -1，因为第一个字符没有前缀。

关于计算

  • 在计算最长公共前后缀时，不能将整个字符串本身作为前缀或后缀。
  • 前缀和后缀必须是字符串的真子串（即不能等于字符串本身）。

字典树 Trie

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
struct trie
{
    int nex[100000][26],cnt;
    bool exist[100000];
    void insert(char*s, int l)
    {
        int p=0;
        for(int i=0;i<l;i++)
        {
            int c=s[i]-'a';
            if(!nex[p][c]) nex[p][c]=++cnt;
            p=nex[p][c];
        }
        exist[p]=true;
    }
    bool find(char *s, int l) 
    {
        int p=0;
        for(int i=0;i<l;i++)
        {
            int c=s[i]-'a';
            if(!nex[p][c])return 0;
            p=nex[p][c];
        }
        return exist[p];
    }
};

树

非递归树的遍历

中根遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void NonRecursiveInOrderTraversal(TreeNode* root) {
    std::stack<TreeNode*> S;
    TreeNode* p = root;

    // Traverse the tree
    while (p != NULL || !S.empty()) {
        // Reach the leftmost node
        while (p != NULL) {
            S.push(p);
            p = p->left;
        }

        // Process the top node in the stack
        if (!S.empty()) {
            p = S.top();
            S.pop();
            std::cout << p->data << " ";  // Visit the node

            // Move to the right child
            p = p->right;
        }
    }
}

伪代码：

Algorithm 
NonRecursiveInOrderTraversal:
Input: A binary tree with root node `t`
Output: Print the nodes in the tree in in-order sequence

Step 1: Initialize stack `S` and pointer `p = t`

Step 2: While `p` is not NULL:
    - Push node `p` onto stack `S`
    - Set `p = p.Left` (Move to the left child)

Step 3: While stack `S` is not empty:
    - Pop the top node `p` from stack `S`
    - Print `p.Data`
    - Set `p = p.Right` (Move to the right child)
    - If `p` is not NULL, go to Step 2
EndAlgorithm

后根遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void NonRecursivePostOrderTraversal(TreeNode* root) {
    if (!root) return;
    
    std::stack<std::pair<TreeNode*, int>> S;  // Stack to store node and its state (0: left, 1: right, 2: visited)
    TreeNode* p = root;
    S.push({p, 0});  // Start from the root node with state 0
    
    while (!S.empty()) {
        p = S.top().first;
        int i = S.top().second;
        S.pop();
        
        if (i == 0) {  // Left child state
            S.push({p, 0});  // Revisit the node after processing left and right children
            if (p->left != NULL) {
                S.push({p->left, 0});  // Visit the left child
            } else {
                S.push({p, 1});  // No left child, move to right child directly
            }
        }
        else if (i == 1) {  // Right child state
            if (p->right != NULL) {
                S.push({p->right, 0});  // Visit the right child
            } else {
                S.push({p, 2});  // No right child, directly visit the node
            }
        }
        else if (i == 2) {  // Visited both left and right children
            std::cout << p->data << " ";  // Visit the node (print data)
        }
    }
}

伪代码：

Algorithm
NonRecursivePostOrderTraversal:
Input: A binary tree with root node `t`
Output: Print the nodes in the tree in post-order sequence

Step 1: Initialize stack `S`
Step 2: Set the initial node `p = t` and state `i = 0` (state 0 for left child, 1 for right child, 2 for visiting)
Step 3: While the stack `S` is not empty:
    - Pop the top element `(p, i)` from stack `S`
    - If `i == 0` (left child):
        - Push `(p, 0)` to stack `S` (revisit the node)
        - If `p.Left` is not NULL, push `(p.Left, 0)` to stack `S` (visit left child)
    - If `i == 1` (right child):
        - If `p.Right` is not NULL, push `(p.Right, 0)` to stack `S` (visit right child)
    - If `i == 2` (visited both left and right children):
        - Print `p.Data` (visit the node)
EndAlgorithm

线索二叉树

Huffman树

为了使问题的处理更为方便，每当原二叉树中出现空子树时，就增加特殊的结点——空树叶，由此生成的二叉树称为扩充二叉树。规定空二叉树的扩充二叉树只有一个方形结点。圆形结点称为内结点 ，方形结点称为外结点。扩充二叉树每一个内结点都有两个儿子，每一个外结点没有儿子。

扩充二叉树的外通路长度定义为从根到每个外结点的路径长度之和，内通路长度定义为从根到每个内结点的路径长度之和。给扩充二叉树中nn个外结点赋上一个实数，称为该结点的权。树的加权外通路长度定义为：

WPL=∑i=1nwiLi\text{WPL}=\sum_{i=1}^{n} w_i L_i

在外结点权值分别为 w0,w1...wn−1w_0,w_1...w_{n-1}的扩充二叉树中，加权外通路长度最小的扩充二叉树称为最优二叉树，即Huffman树。

建立Huffman树：

  • 利用堆（优先队列）：复杂度O(nlog⁡n)O(n\log n)
  • 把结点分成两类：原始和生成，每种都递增两个递增序列取最小，数组或队列均可，建议数组，时间复杂度O(n)O(n)。

总编码长度=WPL总编码长度=\text{WPL}

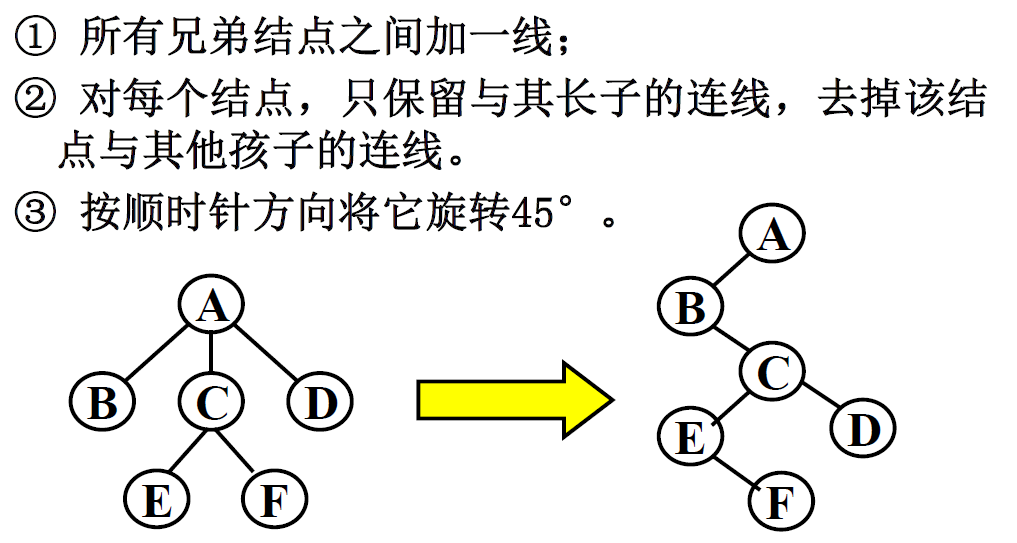
树、二叉树和森林

树和二叉树的转换

树和二叉树的转换

  1. 每个结点的大孩子作为对应二叉树该结点的
    左孩子

  2. 每个结点的其它孩子形成对应二叉树该结点
    左孩子的右链；

这样，在对应的二叉树中，每个结点的左孩子
是其原树结点的大孩子，右孩子是其原树结点
的大兄弟（下一兄弟）。

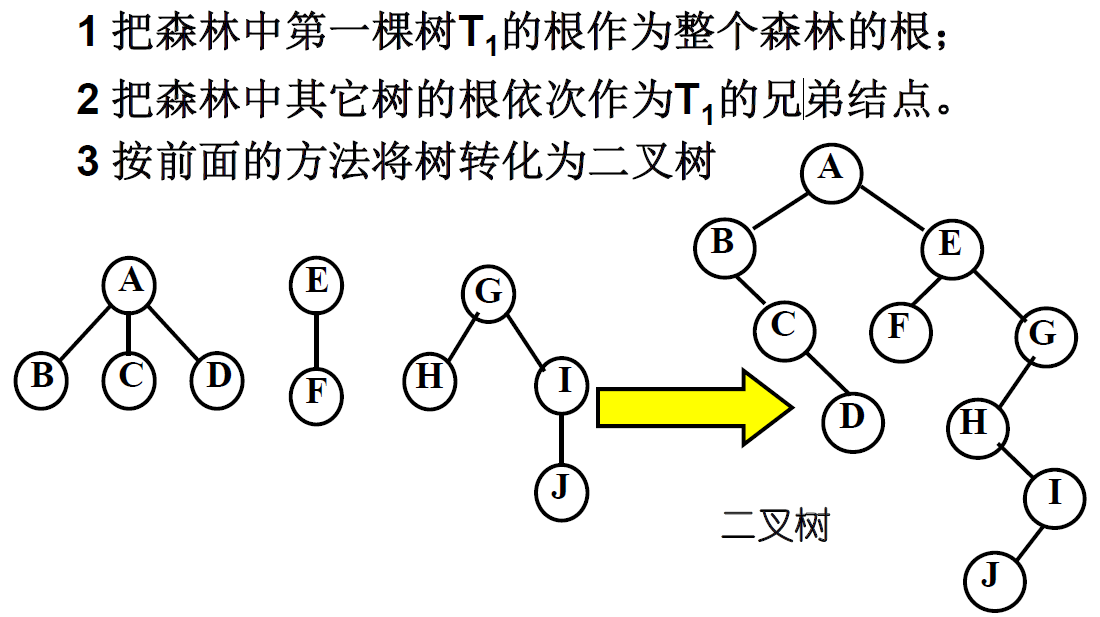
森林和二叉树的转换

森林和二叉树的转换

由森林(d)转换成二叉树(a)之后，二叉树的根是第一棵树的根，二叉树的左子树是由第一棵树的诸子树转换来的，二叉树的右子树是由第二棵树和第三棵树转换来的。

树的遍历

定理

如果已知一个树的先根序列和每个结点相应的次数(度)则能唯一确定该树的结构。

证明

用数学归纳法:

1.若树中只有一个结点 定理显然成立 。

2.假设树中结点个数小于 n(n≥2)n(n \geq 2) 时定理成立。
当树中有nn个结点时，由树的先根序列可知，第一个结点是根结点，设该结点的次数为 k,(k≥1)k,(k\geq1) 因此根结点有 kk个子树。第一个子树排在最前面 第 kk个子树排在最后面并且每个子树的结点个数小于nn。由归纳假设可知 每个子树可以唯一确定 从而整棵树的树形可以唯一确定。

概念辨析

图论

图的存储

邻接矩阵和邻接链表

存储表示空间复杂度求顶点的度判定(vi,vj)(v_i,v_j)求边数
邻接矩阵唯一O(n2)O(n^2) 稠密图O(n)O(n)O(1)O(1)O(n2)O(n^2)
邻接链表不唯一；取决于边的输入顺序和链接次序O(n+e)O(n+e) 稀疏图无向图O(n)O(n)，有向图O(n+e)O(n+e)O(n)O(n)O(n+e)O(n+e)

前向星

1
2
3
4
5
6
7
8
9
10
11
// head[u] 和 cnt 的初始值都为 -1
void add(int u, int v) {
  nxt[++cnt] = head[u];  // 当前边的后继
  head[u] = cnt;         // 起点 u 的第一条边
  to[cnt] = v;           // 当前边的终点
}

// 遍历 u 的出边
for (int i = head[u]; ~i; i = nxt[i]) {  // ~i 表示 i != -1
  int v = to[i];
}
空间复杂度判定(vi,vj)(v_i,v_j)遍历点 uu 的所有出边遍历整张图
O(m)O(m)O(d+(u))O(d^+(u))O(d+(u))O(d^+(u))O(n+m)O(n+m)

最短路

Floyd算法

生成树

树的等价性定义（图论）：

令G=(V,E)G = (V,E) 是一个无向图，下面描述是等价的：

1.GG 是自由树

2.GG 无环，且 ∣E∣=∣V∣−1| E | = | V |- 1

3.GG 连通，且 ∣E∣=∣V∣−1| E | = | V |- 1

4.GG 无环，但增加任意一条边后均有环

5.GG 连通，但移除任意一条边后均不连通

6.GG 中任意两点之间有唯一一条路

一种策略：逐步生成，每次确定 MST 的一条边

过程：管理边集 AA 。 AA 初始空，循环加 n−1n-1 条边。

增加边前， AA 都是某棵 MST 的子集（循环不变式）。
增加边时，选择一条边(u,v)(u,v)加入 AA 中，使 AA 不违反循环不变式，即 A∪(u,v)A\cup (u,v) 也是某棵 MST 的子集。

(u,v)(u,v)加入不破坏循环不变式，称其为AA的安全边

奥妙：安全边必然存在。关键：寻找安全边。

Prim算法(适合稠密图)

设G=(V,E,W)G=(V,E,W) 为连通网 TETE 是 GG 的最小生成树 MST的边的集合，UU 为 MST 顶点集。

  1. 初始化： U=u0,u0∈V,TE=∅U={u_0},u_0\in V,TE=\emptyset

  2. 找到满足weight(u,v)=min{weight(u1,v1)∣u1∈U,v1∈V−U}\text{weight}(u,v)= \text{min} \{\text{weight}(u_1 ,v_1)|u_1\in U, v_1\in V-U\},的边把它并入 TETE 同时 vv 并入 UU

  3. 反复执行 2,直至 V=UV=U 算法结束

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
priority_queue<S> q;
int dis[N];
bool vis[N];

int res = 0, cnt = 0;

void Prim() {
  memset(dis, 0x3f, sizeof(dis));
  dis[1] = 0;
  q.push({1, 0});
  while (!q.empty()) {
    if (cnt >= n) break;
    int u = q.top().u, d = q.top().d;
    q.pop();
    if (vis[u]) continue;
    vis[u] = true;
    ++cnt;
    res += d;
    for (int i = h[u]; i; i = e[i].x) {
      int v = e[i].v, w = e[i].w;
      if (w < dis[v]) {
        dis[v] = w, q.push({v, w});
      }
    }
  }
}

时间复杂度为 O(n2)O(n^2)

使用堆优化，可达到 O(elog⁡n)O(e \log n)

Kruskal算法(适合稀疏图)

边表+并查集实现：

  • 排序： O(elog⁡e)O( e\log e)

  • 判环： O(eα(e))O(e\alpha(e))

  • 整体时间复杂度 O(elog⁡e)O( e\log e)

堆实现

  • O(elog⁡e)O( e \log e)

拓扑排序

概念

AOV 网：用顶点表示活动，用有向边表示活动之间的先后关系，称这样的有向图为 AOV 网 (Activity On Vertex)。

拓扑序列：AOV 网中的所有顶点的一个线性序列，要求：如果在有向边 <Vi,Vj><V_i,V_j >，那么在序列中 ViV_i必位于 VjV_j 之前。

拓扑排序：构造 AOV 网的拓扑序列的过程称作拓扑排序

二级结论

任意图的拓扑序列不一定存在。例如，存在回路的 AOV 网就无法找到拓扑序列。因为出现了有向环，则意味着某项活动以自己作为先决条件。

有向无环图（DAG）一定存在拓扑序列。

拓扑排序与环的关系：有向图中，可拓扑排序等价于无环。

关键路径

关键路径： AOE 网中具有最大长度的路径。

关键活动：不得延期的活动。

关键活动是关键路径上的活动；关键路径是从源点到汇点由关键活动构成的路径。

最早开始时间veve：按拓扑序递推，

ve(k)={0,if k=1max⁡{ve(j)+weight(<j,k>)},if <vj,vk>∈E(G)ve(k) = \begin{cases} 0, & \text{if } k = 1 \\ \max \{ ve(j) + \text{weight}(<j, k>) \}, & \text{if } <v_j, v_k> \in E(G) \end{cases}

最晚开始时间vlvl：按拓扑序逆推，

vl(k)={ve(n),if k=nmin⁡{vl(j)−weight(<k,j>)},if <vk,vj>∈E(G)vl(k) = \begin{cases} ve(n), & \text{if } k = n \\ \min \{ vl(j) - \text{weight}(<k, j>) \}, & \text{if } <v_k, v_j> \in E(G) \end{cases}

关键活动： vl(i)=ve(i)vl(i)=ve(i)，表示活动 aia_i是没有时间余量的关键活动。

强联通分量

有向图中如果两个点能互相可及（或连通）则称这两个点强连通。

有向图 GG 中任意两点互相可及（或连通） ，则称GG 是强连通图。

有向图 GG 的极大强连通子图，称为强连通分量（SCC,Strongly Connected Component）。

Tarjan算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
const int MAXN = 1000; // 最大节点数
vector<int> adj[MAXN]; // 邻接表存储图
int DFN[MAXN], Low[MAXN]; // DFN[u]：节点u的访问顺序，Low[u]：节点u能追溯到的最早节点
bool inStack[MAXN]; // 记录节点是否在栈中
stack<int> stk; // 用于存储当前路径上的节点
int Index = 0; // 全局索引，用于分配DFN值

void tarjan(int u) {
    DFN[u] = Low[u] = ++Index; // 初始化DFN和Low
    stk.push(u); // 将当前节点压入栈
    inStack[u] = true; // 标记节点在栈中

    // 遍历所有邻接节点
    for (int v : adj[u]) {
        if (!DFN[v]) { // 如果节点v未被访问过
            tarjan(v); // 递归访问v
            Low[u] = min(Low[u], Low[v]); // 更新Low[u]
        } else if (inStack[v]) { // 如果节点v在栈中
            Low[u] = min(Low[u], DFN[v]); // 更新Low[u]
        }
    }

    // 如果u是强连通分量的根
    if (DFN[u] == Low[u]) {
        cout << "Strongly Connected Component: ";
        while (true) {
            int v = stk.top(); // 取出栈顶节点
            stk.pop(); // 弹出栈顶节点
            inStack[v] = false; // 标记节点不在栈中
            cout << v << " "; // 输出节点
            if (v == u) break; // 直到当前节点u被弹出
        }
        cout << endl;
    }
}

类似 DFS，如果求全图的SCC，每次选择一个未被访问的顶点u运行Tarjan算法。

DFN数组可作访问标志

inStack数组：顶点在栈中标志

Tarjan算法中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为 O(n+e)O(n+e)。

查找

概念

术语意义
查找表是由同一类型的数据元素构成的集合
关键词可标识数据元素的域
查找在查找表中找出满足条件的数据元素
查找结果查找成功、查找失败
查找与插入查找失败后，插入关键词新记录
平均查找长度找一个结点所作的平均比较次数（衡量一个查找算法优劣的主要标准）

顺序查找

传统线性查找：

1
2
3
4
5
6
int sFind(int A[], int N, int K) {
    for (int i = 0; i < N; i++) {
        if (A[i] == K) return i; // 每次循环需要检查 i < N 和 A[i] == K
    }
    return -1;
}

引入监视哨：

1
2
3
4
5
6
int qFind(int A[], int N, int K) {
    A[N] = K; // 设置监视哨
    int i = 0;
    while (A[i] != K) i++; // 只需检查 A[i] == K
    return i < N ? i : -1;
}

引入监视哨后不需要检查循环的边界条件，快了20%。

  • 成功查找的平均查找长度：约0.5n0.5n
  • 查找失败的查找长度：n+1n+1
  • 平均时间复杂度：O(n)O(n)

二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int bFind(int a[], int N, int K) {
    int s = 0;          // 起始位置
    int e = N - 1;      // 结束位置
    int i;              // 中间位置

    while (s <= e) {
        i = (s + e) >> 1; // 使用位运算计算中间位置，等价于 (s + e) / 2
        if (a[i] == K) {
            return i;    // 找到目标值，返回索引
        } else if (a[i] < K) {
            s = i + 1;   // 目标值在右半部分
        } else {
            e = i - 1;   // 目标值在左半部分
        }
    }
    return -1;          // 未找到目标值，返回-1
}

优化

二叉查找树

二叉查找树 （二叉搜索树、二叉排序树 ）：BST是一棵可为空的二叉树；若BST非空，则其中根遍历序列按关键词递增排列。 对半查找、Fibonacci查找等都对应一棵隐
式的二叉查找树。

  • BST 可以作优先级队列：
    • 优先级队列中的元素具有优先级
    • 优先级队列的操作：取最值、删最值、插入、修改
  • BST 也可以作字典：
    • 字典是key-value对的集合。也称为关联数组（associative array）或映射（map）。
    • 字典的操作：查找、插入、删除。

一个无序序列，可通过构造一棵二叉查找树而成为有序序列，这被称为二叉查找树的顺序属性。

二叉查找树会因输入文件的记录顺序不同，而有不同的形态。对包含NN个记录的集合，其对应的关键词有NN种不同的排列，可构成(N2N)/(N+1)\binom{N}{2N}/(N+1)棵不同的二叉查找树。

特殊情况下，会产生退化二叉查找树，从而使最
坏情况查找时间达O(N)O(N)。

关键算法：寻找前驱或后继，

1
2
3
4
5
6
7
8
9
10
11
算法 Successor(x)
/*在 BST 中找 x 的后继*/
S1[有右儿子，向下找]
if(x.rLink != NULL)
    return FindMin(x.rLink)

S2[否则向上找，找到最近的祖先并在其左子树中]
y = x.parent
while(y != NULL && x == y.rLink)
    x = y, y = x.parent
return y

平衡树

一棵 nn个不同关键字的随机构建的二叉搜索树的期望高度为 O(log⁡n)O(\log n)

为了避免二叉搜索树退化成线性表，解决方案有：

  • 随机文件
  • 给定各个查找情况的概率，建立Huffman树
  • AVL树等平衡树：控制树形维护一棵形态较好的二叉查找树（近似最优）

对于二叉搜索树来说，常见的平衡性的定义是指：以 T 为根节点的树，每一个结点的左子树和右子树高度差最多为 1。

线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <bits/stdc++.h>
using namespace std;

template <typename T>
class SegTree
{
    vector<T> tree,lazy;
    vector<T> *arr;
    int n,root,n4,end;

    void maintain(int cl,int cr,int p)
    {
        int cm=cl+(cr-cl)/2;
        if(cl!=cr&&lazy[p])
        {
            lazy[p*2]+=lazy[p];
            lazy[p*2+1]+=lazy[p];
            tree[p*2]+=lazy[p]*(cm-cl+1);
            tree[p*2+1]+=lazy[p]*(cr-cm);
            lazy[p]=0;
        }
    }

    T range_sum(int l,int r,int cl,int cr,int p) 
    {
        if(l<=cl&&cr<=r) return tree[p];
        int m=cl+(cr-cl)/2;
        T sum=0;
        maintain(cl,cr,p);
        if(l<=m) sum+=range_sum(l,r,cl,m,p*2);
        if(r>m) sum+=range_sum(l,r,m+1,cr,p*2+1);
        return sum;
    }

    void range_add(int l,int r,T val,int cl,int cr,int p) 
    {
        if(l<=cl&&cr<=r) 
        {
            lazy[p]+=val;
            tree[p]+=(cr-cl+1)*val;
            return;
        }
        int m=cl+(cr-cl)/2;
        maintain(cl,cr,p);
        if(l<=m) range_add(l,r,val,cl,m,p*2);
        if(r>m) range_add(l,r,val,m+1,cr,p*2+1);
        tree[p]=tree[p*2]+tree[p*2+1];
    }

    void build(int s,int t,int p) 
    {
        if(s==t)
        {
            tree[p]=(*arr)[s];
            return;
        }
        int m=s+(t-s)/2;
        build(s,m,p*2);
        build(m+1,t,p*2+1);
        tree[p]=tree[p*2]+tree[p*2+1];
    }

 public:
    explicit SegTreeLazyRangeAdd<T>(vector<T> v) 
    {
        n=v.size();
        n4=n*4;
        tree=vector<T>(n4,0);
        lazy=vector<T>(n4,0);
        arr=&v;
        end=n-1;
        root=1;
        build(0,end,1);
        arr=nullptr;
    }

    void show(int p,int depth=0) 
    {
        if(p>n4||tree[p]==0) return;
        show(p*2,depth+1);
        for(int i=0;i<depth;++i) putchar('\t');
        printf("%d:%d\n",tree[p],lazy[p]);
        show(p*2+1,depth+1);
    }

    T range_sum(int l,int r) { return range_sum(l,r,0,end,root);}

    void range_add(int l,int r,T val) { range_add(l,r,val,0,end,root);}
};

红黑树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
typedef long long ll;
const int N=1e6+5;
struct node 
{
    int key;
    bool color;
    node *l,*r,*fa;
    node(int key):key(key),color(0),l(nullptr),r(nullptr),fa(nullptr) {}
};

class rbTree 
{
public:
    node* root;
    node* tnull;
    rbTree() 
 {
  tnull=new node(-1);
        tnull->color=1;
        tnull->l=nullptr;
  tnull->r=nullptr;
  root=tnull;
 }
    void init() 
 {
        tnull=new node(-1);
        tnull->color=1;
        tnull->l=tnull->r=nullptr;
    }
    void lrotate(node* x) 
 {
        node* y=x->r;
        x->r=y->l;
        if(y->l!=tnull) y->l->fa=x;

        y->fa=x->fa;
        if(x->fa==nullptr)
            root=y;
        else if(x==x->fa->l)
            x->fa->l=y;
        else
            x->fa->r=y;

        y->l=x;
        x->fa=y;
    }
    void rrotate(node* x) 
 {
        node* y=x->l;
        x->l=y->r;
        if(y->r!=tnull) y->r->fa=x;

        y->fa=x->fa;
        if(x->fa==nullptr)
            root=y;
        else if(x==x->fa->r)
            x->fa->r=y;
        else
            x->fa->l=y;

        y->r=x;
        x->fa=y;
    }
    void fix(node* k) 
 {
        while(k->fa&&!k->fa->color) 
  {
            if(k->fa==k->fa->fa->l) 
   {
                node* tmp=k->fa->fa->r;
                if(tmp&&!tmp->color) 
    {
                    k->fa->color=1;
                    tmp->color=1;
                    k->fa->fa->color=0;
                    k=k->fa->fa;
                }
    else 
    {
                    if(k==k->fa->r) 
     {
                        k=k->fa;
                        lrotate(k);
                    }
                    k->fa->color=1;
                    k->fa->fa->color=0;
                    rrotate(k->fa->fa);
                }
            } 
   else 
   {
                node* tmp=k->fa->fa->l;
                if(tmp&&!tmp->color) 
    {
                    k->fa->color=1;
                    tmp->color=1;
                    k->fa->fa->color=0;
                    k=k->fa->fa;
                } 
    else 
    {
                    if(k==k->fa->l) 
     {
                        k=k->fa;
                        rrotate(k);
                    }
                    k->fa->color=1;
                    k->fa->fa->color=0;
                    lrotate(k->fa->fa);
                }
            }
        }
        root->color=1;
    }
    void ins(int key) 
 {
        node* temp=new node(key);
        temp->fa=nullptr;
        temp->key=key;
        temp->l=tnull;
        temp->r=tnull;
        temp->color=0;

        node* y=nullptr;
        node* x=root;

        while(x!=tnull) 
  {
            y=x;
            if(temp->key<x->key) x=x->l;
            else x=x->r;
        }
        temp->fa=y;
        if(y==nullptr) root=temp;
        else if(temp->key<y->key) y->l=temp;
        else y->r=temp;
        if(temp->fa==nullptr) 
  {
            temp->color=1;
            return;
        }
        if(temp->fa->fa==nullptr) return;
        fix(temp);
    }
    void print(node* root) 
 {
        if(root==tnull) 
  {
            cout<<"-1 B"<<endl;
            return;
        }
        cout<<root->key<<" "<<(root->color==0?"R":"B")<<endl;
        print(root->l);
        print(root->r);
    }
};

int main() 
{
 ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n;
    cin>>n;
    rbTree t;
    for(int i=0;i<n;i++) 
 {
        int val;
        cin>>val;
        t.ins(val);
    }
    t.print(t.root);
}

Treap树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
#include <iostream>
using namespace std;
const int MAXN=100005;
const int INF=1<<30;
int n;

struct treap 
{
    int l[MAXN],r[MAXN],val[MAXN],rnd[MAXN],size_[MAXN],w[MAXN];
    int sz,ans,rt;
    void pushup(int x) { size_[x]=size_[l[x]] + size_[r[x]] + w[x];}
    void lrotate(int &k) 
    {
        int tree=r[k];
        r[k]=l[tree];
        l[tree]=k;
        size_[tree]=size_[k];
        pushup(k);
        k=tree;
    }

    void rrotate(int &k) 
    {
        int tree=l[k];
        l[k]=r[tree];
        r[tree]=k;
        size_[tree]=size_[k];
        pushup(k);
        k=tree;
    }

    void insert(int &k,int x) 
    {
        if(!k) {
            sz++;
            k=sz;
            size_[k]=1;
            w[k]=1;
            val[k]=x;
            rnd[k]=rand();
            return;
        }
        size_[k]++;
        if(val[k]==x) 
        {
            w[k]++;
        } else if(val[k] < x) 
        {
            insert(r[k],x);
            if(rnd[r[k]] < rnd[k]) lrotate(k);
        } else {
            insert(l[k],x);
            if(rnd[l[k]] < rnd[k]) rrotate(k);
        }
    }

    bool del(int &k,int x) 
    {
        if(!k) return false;
        if(val[k]==x) 
        {
            if(w[k] > 1) {
                w[k]--;
                size_[k]--;
                return true;
            }
            if(l[k]==0 || r[k]==0) 
            {
                k=l[k] + r[k];
                return true;
            } 
            else if(rnd[l[k]] < rnd[r[k]]) 
            {
                rrotate(k);
                return del(k,x);
            } 
            else 
            {
                lrotate(k);
                return del(k,x);
            }
        } 
        else if(val[k] < x) 
        {
            bool succ=del(r[k],x);
            if(succ) size_[k]--;
            return succ;
        } 
        else 
        {
            bool succ=del(l[k],x);
            if(succ) size_[k]--;
            return succ;
        }
    }

    int queryrank(int k,int x) 
    {
        if(!k) return 0;
        if(val[k]==x)
            return size_[l[k]] + 1;
        else if(x > val[k]) 
        {
            return size_[l[k]] + w[k] + queryrank(r[k],x);
        } 
        else
            return queryrank(l[k],x);
    }

    int querynum(int k,int x) 
    {
        if(!k) return 0;
        if(x<=size_[l[k]])
            return querynum(l[k],x);
        else if(x > size_[l[k]] + w[k])
            return querynum(r[k],x - size_[l[k]] - w[k]);
        else
            return val[k];
    }

    void querypre(int k,int x) 
    {
        if(!k) return;
        if(val[k] < x)
            ans=k,querypre(r[k],x);
        else
            querypre(l[k],x);
    }

    void querysub(int k,int x) 
    {
        if(!k) return;
        if(val[k] > x)
            ans=k,querysub(l[k],x);
        else
            querysub(r[k],x);
    }
}tree;

int main() 
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    srand(114514);
    cin>>n;
    int op,k;
    while(n--)
    {
        cin>>op>>k;
        switch(op)
        {
            case 1:
                tree.insert(tree.rt,k);
                break;
            case 2:
                cout<<tree.querynum(tree.rt,k)<<endl;
                break;
            case 3:
                tree.del(tree.rt,k);
                break;
            default:
                break;
        }
    }
}

散列

散列方法是按关键字编址的一项技术。以关键字KK为自变量, 通过函数h(K)h(K)计算地址，h(K)h(K)称为散列函数。

散列方法不仅是一种快速的查找方法，也是一种重要的存储方式。按散列方式构造的存储结构被称为散列表，散列表中的一个位置也被称为槽。

冲突：K1≠K2K_1\neq K_2，有h(K1)=h(K2)h(K_1)=h(K_2)。没有冲突的散列函数hh 是很不好找的：对于动态数据困难更大。

散列方法核心：散列函数和冲突消解方法

散列函数是均匀的：设KK是从关键词集合中随机选取的一个关键词，则h(K)h(K)以同等概率取区间[0，M−1][0，M−1]中的每一个值，并与其它关键字已散列到哪个槽位无关。通常应使hh与组成KK的所有符号有关。

散列函数

除法散列

h(K)=Kmod  Mh(K)=K\mod M

除数的大小应选择得当，一般取略大于元素个数的素数；除数的性质与h(K)h(K)的值在给定区域中的分布情况和冲突产生的数量均密切相关。除法散列函数是一种简单、常用的构造散列的方法，并且不要求事先知道关键词的分布。

乘法散列

h(K)=⌊M(Kθmod1)⌋h(K) =\lfloor M( K\theta mod1) \rfloor

θ\theta值接近0或1将导致散列地址集中在表的末端，θ\theta取0.618实验效果较好。

冲突消解

拉链法

对hh值域[0,M−1][0 , M−1]中的每个值保持一个链表。

每个链表中存放一组关键词互相冲突的记录，该组关键词有h(K1)=h(K2)=…=h(Kt)h(K1)=h(K2)=…=h(Kt)。

每个链表LIST[i]有一个表头HEAD[i], i=h(K)+1i=h(K)+1. 同一个链表中的记录按某种次序链接在一起。

期望时间复杂度O(1+λ)O(1+\lambda)，空间复杂度O(M+N)O(M+N)

开地址法

插入关键词值为KK的新元素的方法是：从地址h(K)h(K)开始, 按照某种次序探查插入新元素的空位置。其被检查的位置序列称为探查序列。

  • 线性探查
  • 伪随机探查
  • 二次探查
  • 双散列

线性探查法分析

  • 优点: 简单
  • 缺点: 基本聚集（容易使许多元素在散列表中连成一片，从而使探查的次数增加，影响查找效率）
  • 经验：MM一般取NN的5倍

不能简单地将一个元素清除，这会隔离探查序列后面的元素，从而影响后面元素的查找过程。

查找长度

平均查找长度（Average Search Length, ASL） 是二叉搜索树或其他数据结构中，查找操作的平均路径长度的度量。它衡量了查找某个元素所需要的比较次数。

查找操作可以分为两种情况：

  • 查找成功（Successful Search）：即查找到目标元素。
  • 查找失败（Unsuccessful Search）：即没有找到目标元素。

查找成功的平均查找长度 是指，在所有成功查找的情况下，平均需要多少次比较才能找到目标元素。它通常由树的深度（即节点到根的距离）来度量。

计算方法：

  • 对于每个成功查找的节点，我们记录从根节点到该节点的路径长度（即节点的深度）。
  • 查找成功的平均查找长度是所有成功查找的路径长度的平均值。

假设一个二叉搜索树中有 nn 个节点，并且我们从根节点到每个节点的路径长度为 did_i，其中 1≤i≤n1 \leq i \leq n 是每个节点的索引。那么，查找成功的平均查找长度 ASLsuccess\text{ASL}_{\text{success}} 可以通过以下公式计算：

ASLsuccess=1n∑i=1ndi\text{ASL}_{\text{success}} = \frac{1}{n} \sum_{i=1}^{n} d_i

其中，did_i 是第 ii 个节点的深度。

查找失败的平均查找长度 是指，在查找操作没有找到目标元素的情况下，平均需要多少次比较。查找失败时，路径长度是指从根节点到查找失败位置的路径长度，即搜索的终止位置。

假设树的总节点数为 nn，查找失败时，路径长度一般会比查找成功时长，因为失败的查找通常会到达树的某一空子树。计算失败的查找路径长度时，涉及所有可能查找的失败位置。

对于二叉搜索树，查找失败的路径通常与树的结构有很大关系。如果树接近平衡（即树的高度较小），则查找失败时的路径较短。如果树是不平衡的（例如，像链表一样），失败路径可能较长。

ASLfailure=1n+1∑i=1n+1di′\text{ASL}_{\text{failure}} = \frac{1}{n+1} \sum_{i=1}^{n+1} d'_i

其中，di′d'_i 是失败查找的位置的深度，n+1n+1 是树中假设的额外一个失败查找位置（即空子树位置）。这个计算通常需要根据树的具体结构来分析，或者通过模拟来估算。

排序

排序算法复杂度

排序算法时间复杂度 (最优)时间复杂度 (平均)时间复杂度 (最坏)空间复杂度稳定性
冒泡排序O(n)O(n)O(n2)O(n^2)O(n2)O(n^2)O(1)O(1)稳定
选择排序O(n2)O(n^2)O(n2)O(n^2)O(n2)O(n^2)O(1)O(1)不稳定
插入排序O(n)O(n)O(n2)O(n^2)O(n2)O(n^2)O(1)O(1)稳定
归并排序O(nlog⁡n)O(n \log n)O(nlog⁡n)O(n \log n)O(nlog⁡n)O(n \log n)O(n)O(n)稳定
快速排序O(nlog⁡n)O(n \log n)O(nlog⁡n)O(n \log n)O(n2)O(n^2)O(log⁡n)O(\log n)不稳定
堆排序O(nlog⁡n)O(n \log n)O(nlog⁡n)O(n \log n) (建堆O(log⁡n)O(\log n))O(nlog⁡n)O(n \log n)O(1)O(1)不稳定
计数排序O(n+k)O(n + k)O(n+k)O(n + k)O(n+k)O(n + k)O(k)O(k)稳定
桶排序O(n+k)O(n + k)O(n+k)O(n + k)O(n2)O(n^2)O(n+k)O(n + k)稳定
基数排序O(nk)O(nk)O(nk)O(nk)O(nk)O(nk)O(n+k)O(n + k)稳定
希尔排序O(nlog⁡n)O(n \log n)O(n32)O(n^\frac{3}{2})O(n2)O(n^2)O(1)O(1)不稳定

其他数据结构

并查集

时间复杂度：

  • 查找： O(n)O(n)
  • 合并： O(n)O(n)
  • 启发式合并： O(nlog⁡n)O( n\log n )

空间复杂度：O(n)O(n)

课程笔记
#算法 #C++
数据结构课程板子合集&笔记
https://blog.kisechan.space/2024/ds/
作者
Kisechan
发布于
2024年12月9日
更新于
2024年1月2日
许可协议