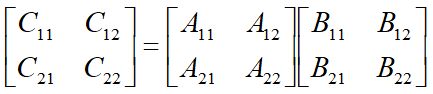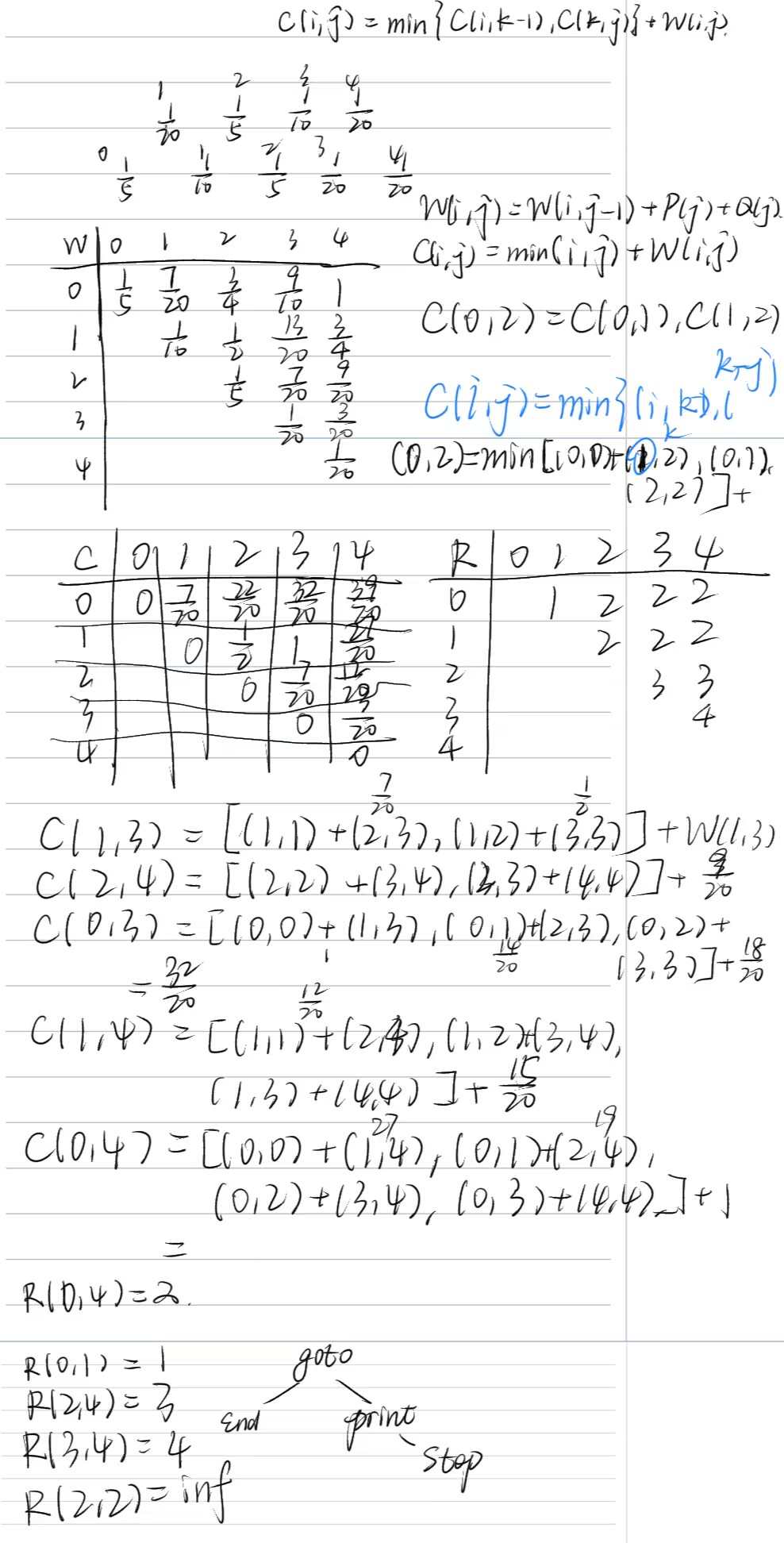导引 算法是解决一确定类问题的任意一种特殊的方法 。不是针对个别、偶然出现的问题,而是为了解决具有相同性质的一系列问题;且同一类问题可以拥有很多不同的算法。
算法的非形式描述:算法就是一组有穷的规则 ,它规定了解决某一特定类型问题的一系列运算。
五个重要特性 例如操作系统,当没有任务时,操作系统并不终止,而是处于等待状态,直到有新的任务启动,因而不是一个算法。
算法学习的内容 算法设计 面对具体问题,运用一些基本设计策略,规划算法。
算法表示 采用SPARKS程序设计语言。
算法确认 证明该算法对所有可能的合法输入,都能给出正确答案。
有这些方法:
穷举法 :测试算法所有可能的合法输入,并验证对于每一个输入,算法的输出是否正确。
数学归纳法 :常用于证明涉及自然数或可以按某种规模递增的问题,适用于具有递归结构或可以按规模递增分析的算法,例如证明某个递归算法对于所有非负整数 n n n
反证法
构造性证明 :直接构造出满足问题要求的解或过程来证明某个命题的正确性,直接展示算法是如何一步步地从输入得到正确输出的。
测试 :通过运行算法并检查其在各种输入下的输出是否正确来验证算法的正确性。测试需要精心设计测试用例。
算法分析 算法分析就是在最好、最坏、平均情况下对时间复杂度 T ( n ) T(n) T ( n ) S ( n ) S(n) S ( n ) n n n
T max ( n ) = max { T ( I ) ∣ s i z e ( I ) = n } T_{\max}(n)=\max\{\:T(I)\mid\mathrm{size}(I){=}n\:\} T m a x ( n ) = max { T ( I ) ∣ size ( I ) = n }
T min ( n ) = min { T ( I ) ∣ s i z e ( I ) = n } T_{\min}(n)=\min\{\:T(I)\mid\mathrm{size}(I){=}n\:\} T m i n ( n ) = min { T ( I ) ∣ size ( I ) = n }
T a v g ( n ) = ∑ size ( I ) = n p ( I ) T ( I ) T_{\mathrm{avg}}(n)=\sum_{\text{size}(I)=n}p(I)T(I) T avg ( n ) = size ( I ) = n ∑ p ( I ) T ( I )
其中, I I I n n n p ( I ) p(I) p ( I )
同一条语句在一个算法中的执行次数称为频率计数。由算法直接确定,与所用的机器无关,且独立于程序设计语言。
语句的时间总量 = 频率计数 × 执行一次该语句所需要的时间 \text{语句的时间总量}=\text{频率计数} \times \text{执行一次该语句所需要的时间} 语句的时间总量 = 频率计数 × 执行一次该语句所需要的时间
算法的执行时间就是构成算法的所有语句的执行时间总量之和。
准确分析出算法数量级的多项式表达式是很困难的,因此一般只对计算时间表达式的最高次项进行渐进表示。
时间的渐进表示 f ( n ) = O ( g ( n ) ) f(n)=O(g(n)) f ( n ) = O ( g ( n ))
f ( n ) = Ω ( g ( n ) ) f(n)=\Omega(g(n)) f ( n ) = Ω ( g ( n ))
f ( n ) = Θ ( g ( n ) ) f(n)=\Theta(g(n)) f ( n ) = Θ ( g ( n ))
f ( n ) f(n) f ( n )
而 g ( n ) g(n) g ( n )
算法的实际运行时间 f ( n ) f(n) f ( n )
算法的渐进增长率 ,即当输入规模 n 趋于无穷大时,运行时间增长的速度,通常是相对稳定的,并且可以用一个与机器和语言无关的简单函数 g ( n ) g(n) g ( n )
常用的求和公式
∑ 1 ≤ i ≤ n 1 = Θ ( n ) ∑ 1 ≤ i ≤ n i = n ( n + 1 ) / 2 = Θ ( n 2 ) ∑ 1 ≤ i ≤ n i 2 = n ( n + 1 ) ( 2 n + 1 ) / 6 = Θ ( n 3 ) \sum_{1\leq i\leq n}1=\Theta(n)\\\sum_{1\leq i\leq n}i=n(n+1)/2=\Theta(n^2)\\\sum_{1\leq i\leq n}i^2=n(n+1)(2n+1)/6=\Theta(n^3) 1 ≤ i ≤ n ∑ 1 = Θ ( n ) 1 ≤ i ≤ n ∑ i = n ( n + 1 ) /2 = Θ ( n 2 ) 1 ≤ i ≤ n ∑ i 2 = n ( n + 1 ) ( 2 n + 1 ) /6 = Θ ( n 3 )
通式:
∑ 1 ≤ i ≤ n i k = n k + 1 k + 1 + n k 2 + 低次项 = Θ ( n k + 1 ) \sum_{1\leq i\leq n}{i}^k=\frac{n^{k+1}}{k+1}+\frac{n^k}2+\text{低次项}=\Theta(n^{k+1}) 1 ≤ i ≤ n ∑ i k = k + 1 n k + 1 + 2 n k + 低次项 = Θ ( n k + 1 )
比较时间复杂度
对于两个函数 f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n )
lim n → ∞ f ( n ) g ( n ) \lim_{n \to \infty} \frac{f(n)}{g(n)} n → ∞ lim g ( n ) f ( n )
如果结果是 0 0 0 f ( n ) = O ( g ( n ) ) f(n) = O(g(n)) f ( n ) = O ( g ( n )) f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) g ( n ) g(n) g ( n ) 如果结果是一个正的有限常数:说明 f ( n ) = Θ ( g ( n ) ) f(n) = \Theta(g(n)) f ( n ) = Θ ( g ( n )) 同阶 。 如果结果是无穷大:说明 f ( n ) = Ω ( g ( n ) ) f(n) = \Omega(g(n)) f ( n ) = Ω ( g ( n )) f ( n ) f(n) f ( n ) O ( 1 ) < O ( log log n ) < O ( log n ) < O ( ( log n ) k ) ( k > 1 ) < O ( n ε ) ( 0 < ε < 1 ) < O ( n ) < O ( n log n ) < O ( n k ) ( k > 1 ) < O ( c n ) ( c > 1 , 如 2 n ) < O ( n ! ) < O ( n n ) \begin{align*}O(1)&< O(\log \log n) \\&< O(\log n) \\&< O((\log n)^k) \quad (k > 1) \\&< O(n^{\varepsilon}) \quad (0 < \varepsilon < 1) \\&< O(n) \\&< O(n \log n) \\&< O(n^k) \quad (k > 1) \\&< O(c^n) \quad (c > 1, \text{如 } 2^n) \\&< O(n!) \\&< O(n^n)\end{align*} O ( 1 ) < O ( log log n ) < O ( log n ) < O (( log n ) k ) ( k > 1 ) < O ( n ε ) ( 0 < ε < 1 ) < O ( n ) < O ( n log n ) < O ( n k ) ( k > 1 ) < O ( c n ) ( c > 1 , 如 2 n ) < O ( n !) < O ( n n )
另外:
O ( α ( n ) ) < O ( 1 ) , 反 Ackermann 函数 O ( A ( n , n ) ) > O ( n n ) , Ackermann 函数 \begin{align*}O(\alpha(n)) &< O(1), \quad \text{反 Ackermann 函数} \\O(A(n, n)) &> O(n^n), \quad \text{Ackermann 函数}\end{align*} O ( α ( n )) O ( A ( n , n )) < O ( 1 ) , 反 Ackermann 函数 > O ( n n ) , Ackermann 函数
例如:
1 2 3 4 5 count = 0
总操作次数:
T = ∑ i = 1 log n ∑ j = i i + 5 ∑ k = 1 i 1 = ∑ i = 1 log n ∑ j = i i + 5 i = ∑ i = 1 log n 6 i = 6 ∑ i = 1 log n i T = \sum_{i=1}^{\log n} \sum_{j=i}^{i+5} \sum_{k=1}^{i} 1 = \sum_{i=1}^{\log n} \sum_{j=i}^{i+5} i = \sum_{i=1}^{\log n} 6i = 6 \sum_{i=1}^{\log n} i T = i = 1 ∑ l o g n j = i ∑ i + 5 k = 1 ∑ i 1 = i = 1 ∑ l o g n j = i ∑ i + 5 i = i = 1 ∑ l o g n 6 i = 6 i = 1 ∑ l o g n i
即:
T = 6 × log n ( log n + 1 ) 2 = 3 log n ( log n + 1 ) T = 6 \times \frac{\log n (\log n + 1)}{2} = 3 \log n (\log n + 1) T = 6 × 2 log n ( log n + 1 ) = 3 log n ( log n + 1 )
总时间复杂度为:
O ( ( log n ) 2 ) \boxed{O((\log n)^2)} O (( log n ) 2 )
上界 f ( n ) = O ( g ( n ) ) f(n)=O(g(n)) f ( n ) = O ( g ( n )) n n n f ( n ) f(n) f ( n ) 小于等于 函数 g ( n ) g(n) g ( n ) g ( n ) g(n) g ( n ) O O O
O ( g ( n ) ) O(g(n)) O ( g ( n ))
O O O
O ( f ( n ) ) + O ( g ( n ) ) = O ( max ( f ( n ) , g ( n ) ) O(f(n))+O(g(n)) = O(\max(f(n), g(n)) O ( f ( n )) + O ( g ( n )) = O ( max ( f ( n ) , g ( n ))
若 f ′ ( n ) = O ( f ( n ) ) f'(n) = O(f(n)) f ′ ( n ) = O ( f ( n )) c 1 c_1 c 1 n 1 n_1 n 1 n ≥ n 1 n \ge n_1 n ≥ n 1 f ′ ( n ) ≤ c 1 ⋅ f ( n ) f'(n) \le c_1 \cdot f(n) f ′ ( n ) ≤ c 1 ⋅ f ( n )
若 g ′ ( n ) = O ( g ( n ) ) g'(n) = O(g(n)) g ′ ( n ) = O ( g ( n )) c 2 c_2 c 2 n 2 n_2 n 2 n ≥ n 2 n \ge n_2 n ≥ n 2 g ′ ( n ) ≤ c 2 ⋅ g ( n ) g'(n) \le c_2 \cdot g(n) g ′ ( n ) ≤ c 2 ⋅ g ( n )
考虑 f ′ ( n ) + g ′ ( n ) f'(n) + g'(n) f ′ ( n ) + g ′ ( n ) n ≥ max { n 1 , n 2 } n \ge \max\{n_1, n_2\} n ≥ max { n 1 , n 2 }
f ′ ( n ) + g ′ ( n ) ≤ c 1 ⋅ f ( n ) + c 2 ⋅ g ( n ) f'(n) + g'(n) \le c_1 \cdot f(n) + c_2 \cdot g(n) f ′ ( n ) + g ′ ( n ) ≤ c 1 ⋅ f ( n ) + c 2 ⋅ g ( n )
由于 p ( n ) = max { f ( n ) , g ( n ) } p(n) = \max\{f(n), g(n)\} p ( n ) = max { f ( n ) , g ( n )} f ( n ) ≤ p ( n ) f(n) \le p(n) f ( n ) ≤ p ( n ) g ( n ) ≤ p ( n ) g(n) \le p(n) g ( n ) ≤ p ( n ) c 1 > 0 c_1 > 0 c 1 > 0 c 2 > 0 c_2 > 0 c 2 > 0 c 1 ⋅ f ( n ) ≤ c 1 ⋅ p ( n ) c_1 \cdot f(n) \le c_1 \cdot p(n) c 1 ⋅ f ( n ) ≤ c 1 ⋅ p ( n ) c 2 ⋅ g ( n ) ≤ c 2 ⋅ p ( n ) c_2 \cdot g(n) \le c_2 \cdot p(n) c 2 ⋅ g ( n ) ≤ c 2 ⋅ p ( n ) c 1 ⋅ f ( n ) + c 2 ⋅ g ( n ) ≤ c 1 ⋅ p ( n ) + c 2 ⋅ p ( n ) = ( c 1 + c 2 ) ⋅ p ( n ) c_1 \cdot f(n) + c_2 \cdot g(n) \le c_1 \cdot p(n) + c_2 \cdot p(n) = (c_1 + c_2) \cdot p(n) c 1 ⋅ f ( n ) + c 2 ⋅ g ( n ) ≤ c 1 ⋅ p ( n ) + c 2 ⋅ p ( n ) = ( c 1 + c 2 ) ⋅ p ( n )
因此,当 n ≥ n 3 = max { n 1 , n 2 } n \ge n_3 = \max\{n_1, n_2\} n ≥ n 3 = max { n 1 , n 2 } f ′ ( n ) + g ′ ( n ) ≤ ( c 1 + c 2 ) ⋅ p ( n ) f'(n) + g'(n) \le (c_1 + c_2) \cdot p(n) f ′ ( n ) + g ′ ( n ) ≤ ( c 1 + c 2 ) ⋅ p ( n ) c 3 = c 1 + c 2 c_3 = c_1 + c_2 c 3 = c 1 + c 2
由于 c 1 c_1 c 1 c 2 c_2 c 2 c 3 c_3 c 3 c 3 c_3 c 3 n 3 n_3 n 3 n ≥ n 3 n \ge n_3 n ≥ n 3 f ′ ( n ) + g ′ ( n ) ≤ c 3 ⋅ max { f ( n ) , g ( n ) } f'(n) + g'(n) \le c_3 \cdot \max\{f(n), g(n)\} f ′ ( n ) + g ′ ( n ) ≤ c 3 ⋅ max { f ( n ) , g ( n )}
O ( f ( n ) ) + O ( g ( n ) ) = O ( f ( n ) + g ( n ) ) O(f(n))+O(g(n)) = O(f(n)+g(n)) O ( f ( n )) + O ( g ( n )) = O ( f ( n ) + g ( n ))
O ( f ( n ) ) O ( g ( n ) ) = O ( f ( n ) g ( n ) ) O(f(n)) O(g(n)) = O(f(n) g(n)) O ( f ( n )) O ( g ( n )) = O ( f ( n ) g ( n ))
如果 g ( n ) = O ( f ( n ) ) g(n) = O(f(n)) g ( n ) = O ( f ( n )) O ( f ( n ) ) + O ( g ( n ) ) = O ( f ( n ) ) O(f(n))+O(g(n)) = O(f(n)) O ( f ( n )) + O ( g ( n )) = O ( f ( n ))
O ( c f ( n ) ) = O ( f ( n ) ) O(cf(n)) = O(f(n)) O ( c f ( n )) = O ( f ( n )) c c c
f ( n ) = O ( f ( n ) ) f(n) = O(f(n)) f ( n ) = O ( f ( n ))
下界 Ω \Omega Ω
Ω ( f ( n ) ) + Ω ( g ( n ) ) = Ω ( min ( f ( n ) , g ( n ) ) \Omega(f(n))+ \Omega(g(n)) = \Omega(\min(f(n), g(n)) Ω ( f ( n )) + Ω ( g ( n )) = Ω ( min ( f ( n ) , g ( n ))
Ω ( f ( n ) ) + Ω ( g ( n ) ) = Ω ( f ( n ) + g ( n ) ) \Omega(f(n))+ \Omega(g(n)) = \Omega(f(n)+g(n)) Ω ( f ( n )) + Ω ( g ( n )) = Ω ( f ( n ) + g ( n ))
Ω ( f ( n ) ) Ω ( g ( n ) ) = Ω ( f ( n ) g ( n ) ) \Omega(f(n)) \Omega(g(n)) = \Omega(f(n) g(n)) Ω ( f ( n )) Ω ( g ( n )) = Ω ( f ( n ) g ( n ))
如果 g ( n ) = Ω ( f ( n ) ) g(n) = \Omega(f(n)) g ( n ) = Ω ( f ( n )) Ω ( f ( n ) ) + Ω ( g ( n ) ) = Ω ( f ( n ) ) \Omega(f(n))+ \Omega(g(n)) = \Omega(f(n)) Ω ( f ( n )) + Ω ( g ( n )) = Ω ( f ( n ))
Ω ( c f ( n ) ) = Ω ( f ( n ) ) \Omega(cf(n)) = \Omega(f(n)) Ω ( c f ( n )) = Ω ( f ( n ))
f ( n ) = Ω ( f ( n ) ) f(n) = \Omega(f(n)) f ( n ) = Ω ( f ( n ))
渐进函数的性质 如果以 Q Q Q
传递性 :∃ f ( n ) = Q ( g ( n ) ) , g ( n ) = Q ( h ( n ) ) ⇒ f ( n ) = Q ( h ( n ) ) \exists f(n)= Q(g(n)), g(n)=Q(h(n)) \Rightarrow f(n)= Q(h(n)) ∃ f ( n ) = Q ( g ( n )) , g ( n ) = Q ( h ( n )) ⇒ f ( n ) = Q ( h ( n ))
反身性 :f ( n ) = Q ( f ( n ) ) f(n)=Q(f(n)) f ( n ) = Q ( f ( n ))
满足加法和乘法的四则运算 :Q ( f ( n ) ∘ g ( n ) ) = Q ( f ( n ) ) ∘ Q ( g ( n ) ) ( ∘ ∈ { + , × } ) Q(f(n)\circ g(n))=Q(f(n))\circ Q(g(n)) \quad (\circ \in \{+, \times\}) Q ( f ( n ) ∘ g ( n )) = Q ( f ( n )) ∘ Q ( g ( n )) ( ∘ ∈ { + , × })
例如,证明 O ( f ( n ) ) O ( g ( n ) ) = O ( f ( n ) g ( n ) ) O(f(n))O(g(n))=O(f(n) g(n)) O ( f ( n )) O ( g ( n )) = O ( f ( n ) g ( n ))
设 f 1 ( n ) = O ( f ( n ) ) f_1(n)=O(f(n)) f 1 ( n ) = O ( f ( n )) n 1 n_1 n 1 c 1 c_1 c 1 n ≥ n 1 n\ge n_1 n ≥ n 1 f 1 ( n ) ≤ c 1 × f ( n ) f_1(n)\le c_1\times f(n) f 1 ( n ) ≤ c 1 × f ( n ) 设 f 2 ( n ) = O ( g ( n ) ) f_2(n)=O(g(n)) f 2 ( n ) = O ( g ( n )) n 2 n_2 n 2 c 2 c_2 c 2 n ≥ n 2 n\ge n_2 n ≥ n 2 f 2 ( n ) ≤ c 2 × g ( n ) f_2(n)\le c_2\times g(n) f 2 ( n ) ≤ c 2 × g ( n ) 当 n ≥ max { n 1 , n 2 } n\geq\max\{n_1,n_2\} n ≥ max { n 1 , n 2 } O ( f ( n ) ) O ( g ( n ) ) = f 1 ( n ) f 2 ( n ) ≤ c 1 f ( n ) × c 2 g ( n ) = c 1 c 2 f ( n ) g ( n ) O(f(n))O(g(n))=f_1(n)f_2(n)\leq{c}_1f(n)\times{c}_2g(n)={c}_1{c}_2f(n)g(n) O ( f ( n )) O ( g ( n )) = f 1 ( n ) f 2 ( n ) ≤ c 1 f ( n ) × c 2 g ( n ) = c 1 c 2 f ( n ) g ( n ) c 0 = c 1 c 2 , n 0 = max { n 1 , n 2 } c_0=c_1c_2, n_0=\max\{n_1,n_2\} c 0 = c 1 c 2 , n 0 = max { n 1 , n 2 } O ( f ( n ) ) O ( g ( n ) ) = O ( f ( n ) g ( n ) ) O(f(n))O(g(n))=O(f(n) g(n)) O ( f ( n )) O ( g ( n )) = O ( f ( n ) g ( n )) 分治法 分治法适用于 n n n 取值相当大 ,直接求解往往非常困难,甚至无法求出的问题。
分治法的核心操作在于:
分 :将 n n n k k k k k k 可独立求解的子问题 。治 :求出子问题的解。合 :在求出子问题的解之后,能找到适当的方法把它们合并成整个问题的解 的情况。子问题的规模不相近 会影响算法效率:
当子问题的规模尽可能相近 时,递归树会更加平衡,这意味着需要进行的递归层数会更少。 如果规模相差很大,会导致工作量分配不均,导致复杂度退化 。 可能影响合并操作的效率 。 考虑快速排序 。如果每次选择的基准元素都能将数组均匀地分成两半,那么快速排序的平均时间复杂度是 O ( n log n ) O(n\log n) O ( n log n ) 导致子问题规模极不平衡 (一个子问题几乎是原问题的大小减一,另一个为空),那么快速排序的时间复杂度会退化到 O ( n 2 ) O(n^2) O ( n 2 )
DANDC 流程 Divide and Conquer,简称 D&C 或 DANDC,指的就是分治策略 或分治算法 这种算法设计范式。
1 2 3 4 5 6 7 8 9 10 11 12 13 procedure DANDC(p,q)
若拆分的子问题规模类似,则时间复杂度为:
T ( n ) = { g ( n ) n 足够小 2 T ( n 2 ) + f ( n ) 否则 T(n)= \begin{cases} g(n) && n\text{足够小}\\ 2T\left(\frac{n}{2}\right) + f(n) && \text{否则} \end{cases} T ( n ) = { g ( n ) 2 T ( 2 n ) + f ( n ) n 足够小 否则
T ( n ) T(n) T ( n ) n n n
g ( n ) g(n) g ( n )
f ( n ) f(n) f ( n ) COMBINE 函数合成原问题解的计算时间
二分查找 一个非降序排列 的数组中查找给定的元素 x x x j j j j j j
我们将查找问题建模为一个输入实例 I = ( n , a 1 , … , a n , x ) I = (n, a_1, \ldots, a_n, x) I = ( n , a 1 , … , a n , x ) n n n a 1 , … , a n a_1, \ldots, a_n a 1 , … , a n x x x
1 2 3 4 5 6 7 8 9 10 11 12 13 14 procedure BINSRCH(A, n, x, j)
正确性证明 检验到参数的每类取值 ,即各类输入:
空数组 (n = 0 n=0 n = 0 x x x x x x x x x 检验到算法的每个分支 A A A n n n x x x A A A
成功查找:n n n 如果 x x x n n n 不成功查找:n + 1 n+1 n + 1 如果 x x x 对于一个有 n n n n + 1 n+1 n + 1 时空复杂度分析 时间分析从成功和不成功查找时的终止性 入手。
时间复杂度 最好情况 最差情况 平均情况 成功查找 Θ ( 1 ) \Theta(1) Θ ( 1 ) Θ ( log N ) \Theta(\log N) Θ ( log N ) Θ ( log N ) \Theta(\log N) Θ ( log N ) 失败查找 Θ ( log N ) \Theta(\log N) Θ ( log N ) Θ ( log N ) \Theta(\log N) Θ ( log N ) Θ ( log N ) \Theta(\log N) Θ ( log N ) 基本二分查找 Θ ( 1 ) \Theta(1) Θ ( 1 ) Θ ( log N ) \Theta(\log N) Θ ( log N ) Θ ( log N ) \Theta(\log N) Θ ( log N )
二分思想下查找的时间复杂度大体上是 Θ ( log N ) \Theta(\log N) Θ ( log N )
1 2 3 4 5 6 7 8 9 10 11 12 13 procedure BINSRCH1(A, n, x, j)
考虑这个 BINSRCH1 函数,即使它要查找的元素恰好在第一次 mid 的位置,算法也不会立即返回。它会继续缩小搜索范围,直到 low 和 high 相邻。最终的判断 if x == A(low) 是在循环结束后进行的 。所以它的最优时间复杂度也是 O ( log n ) O(\log n) O ( log n ) O ( 1 ) O(1) O ( 1 )
在特定条件下,对于在静态的、已排序的数组中进行查找,标准二分查找在基于比较的操作次数上是渐近最优 的,但是在一些场景下可以进一步优化:
插值查找 :
插值查找是对二分查找的改进。它不是简单地取中间位置,而是根据要查找的值在数组中的可能位置进行预测 。它假设数组中的元素是均匀分布的。 在均匀分布 的情况下,插值查找的平均时间复杂度可以达到 O ( log log n ) O(\log\log n) O ( log log n ) 如果数据分布不均匀,插值查找的最坏情况时间复杂度会退化到 O ( n ) O(n) O ( n ) 硬件特性和缓存优化 :
标准的二分查找在每次迭代中访问的内存位置可能相距较远,这可能导致缓存未命中,影响实际运行速度。 一些优化的二分查找变体(例如,尝试在更小的范围内进行搜索,以提高缓存命中率)可能会在实际应用中表现更好,尤其是在处理非常大的数组时。 对于非常小的数组:
当数组非常小时,二分查找的优势并不明显,甚至可能因为计算中间索引等额外开销而比线性查找更慢。在实践中,对于小规模问题,可以直接使用线性查找。 如果查找操作非常频繁,且数组内容不经常变化:
可以考虑构建更复杂的数据结构来优化查找,例如 Hashmap(如果不需要有序性)或更高级的树结构(如 B 树或 Trie 树)。 定理 :若 n n n [ 2 k − 1 , 2 k ) [2^{k-1}, 2^k) [ 2 k − 1 , 2 k )
对于一次成功的查找 ,二分查找算法至多作 k k k 对于一次不成功的查找 ,或者作 k − 1 k-1 k − 1 k k k 当数组大小 n n n 2 k − 1 2^{k-1} 2 k − 1 2 k 2^k 2 k k k k 内结点 终止,不成功查找在外结点 终止。
当 2 k − 1 ≤ n < 2 k 2^{k-1} \le n < 2^k 2 k − 1 ≤ n < 2 k ≤ k \le k ≤ k k k k k + 1 k+1 k + 1 ≤ k − 1 \le k-1 ≤ k − 1 k k k
内部路径长度 I I I 外部路径长度 E E E n n n 内节点数 ,因为可以搜到的数一定在内结点。E = I + 2 n E = I + 2n E = I + 2 n I = Θ ( n log n ) I=\Theta(n\log n) I = Θ ( n log n ) E = Θ ( n log n ) E=\Theta(n\log n) E = Θ ( n log n ) 成功查找的平均比较次数 S ( n ) = ( I / n ) + 1 S(n) = (I/n) + 1 S ( n ) = ( I / n ) + 1 不成功查找的平均比较次数 U ( n ) = E / ( n + 1 ) U(n) = E / (n + 1) U ( n ) = E / ( n + 1 ) S ( n ) = Θ ( U ( n ) ) = Θ ( log n ) S(n) = \Theta(U(n)) = \Theta(\log n) S ( n ) = Θ ( U ( n )) = Θ ( log n ) 算法用了 n n n A A A l o w low l o w h i g h high hi g h m i d mid mi d x x x j j j n + 5 = Θ ( n ) n+5=\Theta(n) n + 5 = Θ ( n )
二元比较树 在二分查找算法中,最核心也是决定时间复杂度的基本运算是——将要查找的元素 x x x A [ m i d ] A[mid] A [ mi d ] 比较 。
其他的操作,例如加法、除法、赋值等,其执行次数与比较次数相比是同阶或更低的。可以用二元比较树模拟比较的过程:
二元比较树中的每个内结点 代表一次将 x x x A [ m i d ] A[mid] A [ mi d ] x < A [ m i d ] x < A[mid] x < A [ mi d ] x > A [ m i d ] x > A[mid] x > A [ mi d ]
从根节点到任何一个节点的路径表示了查找过程中进行的一系列比较 。算法的执行过程实质上就是 x x x A ( m i d ) A(mid) A ( mi d )
graph TD
A(5) --> B(3)
A --> C(8)
B --> D(1)
B --> E(4)
D --> G(0)
C --> H(6)
C --> F(9)
F --> I(10)
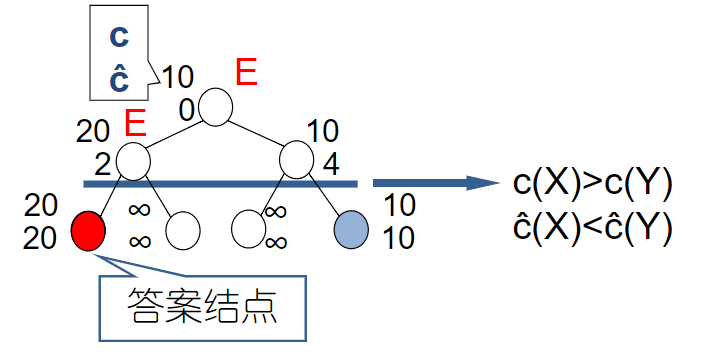
以比较为基础查找的时间下界 对于已排序的 n n n x x x 不存在以比较为基础的查找算法 ,在最坏情况下该算法的计算时间比二分查找算法的计算时间更低 。
任何以比较为基础的查找算法,在最坏情况下至少需要 ⌈ log 2 ( n + 1 ) ⌉ = O ( log n ) \lceil \log_2 (n+1) \rceil=O(\log n) ⌈ log 2 ( n + 1 )⌉ = O ( log n )
类型 以比较为基础解决的时间下界 检索/查找 Ω ( log n ) \boxed{\Omega(\log n)} Ω ( log n ) 排序/分类 Ω ( n log n ) \boxed{\Omega(n \log n)} Ω ( n log n )
三分或多分查找不会带来更优的时间复杂度 。
定理 :设 A ( 1 : n ) A(1:n) A ( 1 : n ) n ( n ≥ 1 ) n (n \ge 1) n ( n ≥ 1 ) A ( 1 ) < A ( 2 ) < … < A ( n ) A(1) < A(2) < … < A(n) A ( 1 ) < A ( 2 ) < … < A ( n ) x ∈ A ( 1 : n ) x \in A(1:n) x ∈ A ( 1 : n ) FIND ( n ) \text{FIND}(n) FIND ( n ) FIND ( n ) ≥ ⌈ log 2 ( n + 1 ) ⌉ \text{FIND}(n) \ge \lceil \log_2(n+1)\rceil FIND ( n ) ≥ ⌈ log 2 ( n + 1 )⌉ FIND ( n ) = Ω ( log n ) \text{FIND}(n)=\Omega(\log n) FIND ( n ) = Ω ( log n )
证明 :
模拟算法的比较树 : 任何基于比较的查找算法都可以用一棵二元比较树来表示其执行过程。内节点与比较 : 每个内节点代表一次对 x x x A A A x < A [ i ] x < A[i] x < A [ i ] x > A [ i ] x > A[i] x > A [ i ] x = A [ i ] x = A[i] x = A [ i ] x < A [ i ] x < A[i] x < A [ i ] x > A [ i ] x > A[i] x > A [ i ] 叶子节点与结果 :成功查找: 如果 x x x A A A n n n x x x A [ 1 ] , A [ 2 ] , … , A [ n ] A[1], A[2], \ldots, A[n] A [ 1 ] , A [ 2 ] , … , A [ n ] 不成功查找: 如果 x x x A A A A A A n + 1 n+1 n + 1 x < A [ 1 ] x < A[1] x < A [ 1 ] A [ 1 ] < x < A [ 2 ] A[1] < x < A[2] A [ 1 ] < x < A [ 2 ] … \ldots … A [ n ] < x A[n] < x A [ n ] < x 最坏情况比较次数与树的深度 : 算法在最坏情况下所需的比较次数等于从根节点到最深的叶子节点的路径长度(树的高度)。因此,FIND ( n ) \text{FIND}(n) FIND ( n ) 内节点数量 : 定理的证明中提到有 n n n x x x A A A n n n n n n n + 1 n+1 n + 1 n + ( n + 1 ) = 2 n + 1 n + (n+1) = 2n+1 n + ( n + 1 ) = 2 n + 1 二叉树的性质 : 如果一棵二叉树的高度为 k k k 2 k 2^k 2 k 应用到查找树 : 为了区分 n + 1 n+1 n + 1 x x x n n n n + 1 n+1 n + 1 高度下界 : 如果一棵二叉树有至少 n + 1 n+1 n + 1 k k k 2 k ≥ n + 1 2^k \ge n+1 2 k ≥ n + 1 k ≥ log 2 ( n + 1 ) k \ge \log_2 (n+1) k ≥ log 2 ( n + 1 ) FIND ( n ) \text{FIND}(n) FIND ( n ) ⌈ log 2 ( n + 1 ) ⌉ \lceil \log_2 (n+1) \rceil ⌈ log 2 ( n + 1 )⌉ 归并排序 给定一个含有 n n n 把它们按非降次序排列 。
一般方法 (直接插入法 ):
1 2 3 for j ← 2 to n do
直接插入排序的思想是将未排序的元素逐个插入到已排序的序列中,保持已排序序列的有序性。
最好情况 :O ( n ) O(n) O ( n ) n − 1 n-1 n − 1 最坏情况 :O ( n 2 ) O(n^2) O ( n 2 ) 分治策略设计归并排序算法 :
分 :将 A ( 1 ) , … , A ( n ) A(1),…,A(n) A ( 1 ) , … , A ( n ) A ( 1 ) , … , A ( ⌈ n / 2 ⌉ ) A(1),…,A(\lceil n/2\rceil) A ( 1 ) , … , A (⌈ n /2 ⌉) A ( ⌈ n / 2 ⌉ + 1 ) , … , A ( n ) A(\lceil n/2\rceil +1),…,A(n) A (⌈ n /2 ⌉ + 1 ) , … , A ( n )
治 :递归调用,将 2 个子集排序。对分解得到的两个子数组分别递归地应用归并排序,直到子数组的长度为 1(长度为 1 的数组自然是有序的),达到递归的基准情况。
合 :将 2 个排好序的子集合并为一个有序集合。这是分治策略的关键一步。将两个已经排序好的子数组合并成一个更大的有序数组。MERGE 算法负责完成这个合并操作.
1 2 3 4 5 6 7 8 9 Procedure MERGESORT(low,high)
MERGESORT 函数是归并排序的递归实现low 和结束索引 high 作为输入。
递归终止条件 : 当 low >= high 时,表示子数组的长度为 0 或 1,此时不需要排序,递归结束。分解 : 计算中间索引 mid,将数组分为 [low, mid] 和 [mid+1, high] 两个子数组。递归求解 : 递归调用 MERGESORT 对这两个子数组进行排序。合并 : 调用 MERGE 函数将排序好的两个子数组 A[low...mid] 和 A[mid+1...high] 合并成一个有序的子数组 A[low...high]。1 2 3 4 5 6 7 8 9 10 11 12 13 integer h, i, j, k, low, mid, high; global A(low : high); local B(low : high)
如果 h <= mid 且 j <= high,那么 B(i) <- min(A(h), A(j)) 如果 h > mid 且 j <= high,那么 B(i) <- A(j) 如果 h <= mid 且 j > high,那么 B(i) <- A(h) Merge 描述了合并两个已排序子数组的基本逻辑。使用两个指针 h 和 j 分别指向两个子数组的起始位置,比较它们指向的元素,将较小的元素放入临时数组 B 中,并移动相应的指针。
归并排序的算法调用过程(MERGESORT 的递归调用)不受输入数组的具体内容 (问题实例)的影响 。无论输入数组是已经排序的、逆序的还是随机的,MERGESORT 都会始终将数组对半分割,并进行相同次数的递归调用,直到子数组长度为 1。
然而,MERGE 函数内部的比较操作次数会受到问题实例的影响。例如,如果两个子数组的元素交错排列,MERGE 中 A[h] <= A[j] 的比较结果会交替变化。但这并不改变 MERGE 函数的时间复杂度,它始终是 O ( h i g h − l o w + 1 ) = O ( n ) O(high - low + 1)=O(n) O ( hi g h − l o w + 1 ) = O ( n )
归并排序算法消耗的时间:
T ( n ) = { a n = 1 , a 为常数 2 T ( n / 2 ) + c n n > 1 , c 为常数 ⇒ T ( n ) = O ( n log n ) T(n)= \begin{cases} a&&n=1,a为常数\\ 2T(n/2)+cn&&n>1,c为常数 \end{cases} \\ \\ \Rightarrow \boxed{T(n)=O(n\log n)} T ( n ) = { a 2 T ( n /2 ) + c n n = 1 , a 为常数 n > 1 , c 为常数 ⇒ T ( n ) = O ( n log n )
当数组只有一个元素时 (n = 1 n=1 n = 1 排序所需的时间是一个常数 a a a 当数组有 n > 1 n > 1 n > 1 解决两个规模为 n / 2 n/2 n /2 的子问题的时间 ,即 2 × T ( n / 2 ) 2\times T(n/2) 2 × T ( n /2 ) 合并两个已排序的子数组的时间 ,即 c n cn c n c c c n 2 \frac{n}{2} 2 n n − 1 n-1 n − 1 在最坏情况下(例如,两个子数组的元素交错排列),需要进行接近 n − 1 n-1 n − 1 h 超过 mid 时)。但这仍然是 O ( n ) O(n) O ( n )
归并排序的递归处理会带来一定的开销(函数调用的压栈和出栈),当子集合的元素个数很少时,继续递归分割可能不如直接使用简单的排序算法,如插入排序更有效,插入排序在小规模数据上通常具有较小的常数因子。这种优化称为切换到插入排序 。
同时,归并排序需要额外的 O ( n ) O(n) O ( n ) B 中)。每次合并后还需要将 B 中的内容复制回 A。消耗了一部分时间。用一个链接数组 LINK(1:n) 代替 B,LINK 中元素为 A 中元素的指针,它指向下一个元素所在的下标位置。
使用链接数组 是一种尝试减少额外空间和复制开销的优化思路。通过维护一个指向下一个元素的指针数组,可以在不实际移动元素的情况下实现有序链表的效果。合并操作可以通过修改指针来实现。这种方法可以减少元素的物理移动,但会引入额外的指针操作和空间来存储链接数组。这种优化在实践中可能更复杂,并且不一定总是比使用辅助数组更高效,尤其是在现代具有良好缓存机制的计算机上,连续内存访问通常更快。 思考:能否采用自底向上的设计方式来取消对系统栈空间的需要 ?
理解 : 递归实现的归并排序需要使用系统栈来保存函数调用的上下文。这在处理非常大的数组时可能导致栈溢出。自底向上的归并排序 是一种非递归的实现方式。它从将每个元素视为一个长度为 1 的已排序子数组开始,然后逐步合并相邻的长度为 1 的子数组,得到长度为 2 的已排序子数组,再合并长度为 2 的子数组得到长度为 4 的,以此类推,直到整个数组都被排序。优点 : 自底向上的归并排序不需要使用递归,因此避免了系统栈的开销,并且通常在某些情况下具有更好的迭代性能。空间复杂度 : 自底向上的归并排序仍然需要 O ( n ) O(n) O ( n ) 定理 :任何以关键字比较为基础的排序算法,最坏情况下的时间下界都是 Ω ( n log n ) \Omega(n\log n) Ω ( n log n )
证明 :
已知 n n n n ! n! n ! 观察二元比较树从根到外节点的每一条路径,分别与一种唯一的排列相对应。则比较树必定至少有 n ! n! n ! T ( n ) T(n) T ( n ) n ≥ 4 n\ge4 n ≥ 4 2 T ( n ) ≥ n ! ≥ ( n 2 ) n 2 ⇒ T ( n ) = O ( n log n ) 2^{T(n)}\ge n! \ge (\frac{n}{2})^{\frac{n}{2}} \Rightarrow T(n)=O(n\log n) 2 T ( n ) ≥ n ! ≥ ( 2 n ) 2 n ⇒ T ( n ) = O ( n log n )
斯特拉森矩阵问题 矩阵 A n × n A_{n×n} A n × n B n × n B_{n×n} B n × n C n × n C_{n×n} C n × n C [ i , j ] C[i,j] C [ i , j ]
C [ i ] [ j ] = ∑ k = 1 n A [ i ] [ k ] B [ k ] [ j ] C[i][j]=\sum_{k=1}^{n}A[i][k]B[k][j] C [ i ] [ j ] = k = 1 ∑ n A [ i ] [ k ] B [ k ] [ j ]
C C C n 2 n^2 n 2 n n n n − 1 n-1 n − 1 O ( n 3 ) O(n^3) O ( n 3 )
如果是将矩阵直接切割成子矩阵,实际上是不能优化的,因为并没有减少子问题的实际数量。
斯特拉森在分治法的基础上,利用技巧减少了子问题的个数。它用 7 个乘法和 10 个加(减)法来算出 7 个 n 2 × n 2 \frac{n}{2}\times\frac{n}{2} 2 n × 2 n C [ i ] [ j ] C[i][j] C [ i ] [ j ] T ( n ) = 8 T ( n 2 ) + c n 2 T(n)=8T(\frac{n}{2})+cn^2 T ( n ) = 8 T ( 2 n ) + c n 2 T ( n ) = 7 T ( n 2 ) + c n 2 T(n)=7T(\frac{n}{2})+cn^2 T ( n ) = 7 T ( 2 n ) + c n 2 O ( n log 7 ) O(n^{\log 7}) O ( n l o g 7 )
二维极大点问题 给定一个包含 n n n S = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) } S = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\} S = {( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n )} p i = ( x i , y i ) ∈ S p_i = (x_i, y_i) \in S p i = ( x i , y i ) ∈ S 极大点 ,当且仅当不存在另一个点 p j = ( x j , y j ) ∈ S p_j = (x_j, y_j) \in S p j = ( x j , y j ) ∈ S i ≠ j i \neq j i = j p i p_i p i x j ≥ x i x_j \ge x_i x j ≥ x i y j ≥ y i y_j \ge y_i y j ≥ y i
如果直接比较每一对点,时间复杂度O ( n 2 ) O(n^2) O ( n 2 )
分 :设计中位线 l l l 递归分为两个子集 S L S_L S L S R S_R S R
治 :分别找出 S L S_L S L S R S_R S R
合 :基于支配规则合并 S L S_L S L S R S_R S R L L L R R R R R R x x x L L L
中位线 :
递归出口:
基于支配规则合并:
对于 S L S_L S L p p p y p y_p y p S R S_R S R y y y p p p S L S_L S L x x x S R S_R S R x x x 使用排序优化后的解法时间复杂度 O ( n log n ) O(n \log n) O ( n log n )
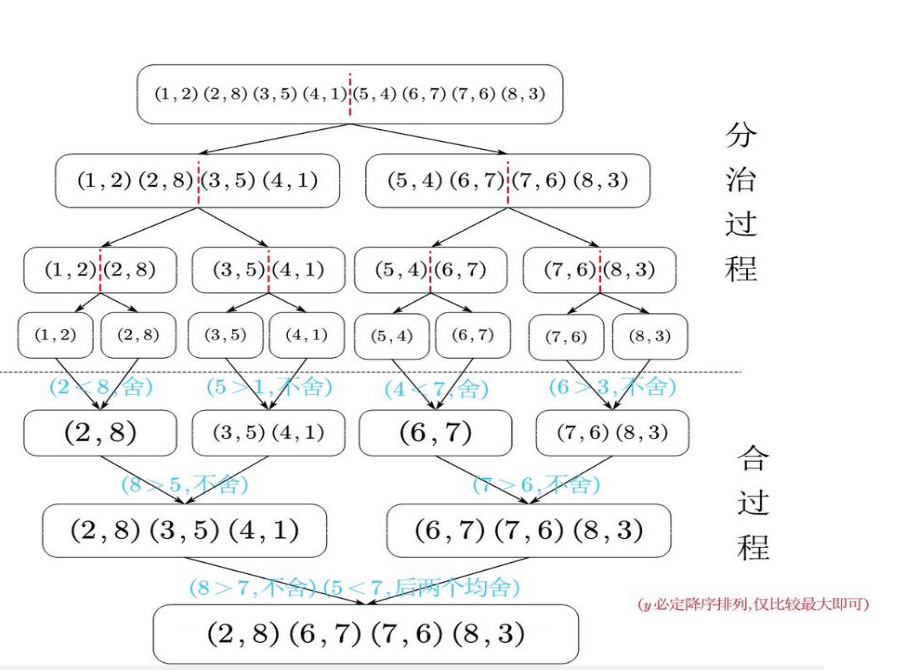
采用分治策略求解二维极大点问题,给出下面实例的求解过程及结果:( 1 , 2 ) , ( 2 , 8 ) , ( 3 , 5 ) , ( 4 , 1 ) , ( 5 , 4 ) , ( 6 , 7 ) , ( 7 , 6 ) , ( 8 , 3 ) (1,2), (2,8), (3,5), (4,1), (5,4), (6,7), (7,6), (8,3) ( 1 , 2 ) , ( 2 , 8 ) , ( 3 , 5 ) , ( 4 , 1 ) , ( 5 , 4 ) , ( 6 , 7 ) , ( 7 , 6 ) , ( 8 , 3 )
首先将所有点按照 x x x x x x y y y
( 1 , 2 ) , ( 2 , 8 ) , ( 3 , 5 ) , ( 4 , 1 ) , ( 5 , 4 ) , ( 6 , 7 ) , ( 7 , 6 ) , ( 8 , 3 ) (1,2), (2,8), (3,5), (4,1), (5,4), (6,7), (7,6), (8,3) ( 1 , 2 ) , ( 2 , 8 ) , ( 3 , 5 ) , ( 4 , 1 ) , ( 5 , 4 ) , ( 6 , 7 ) , ( 7 , 6 ) , ( 8 , 3 )
分 :找出垂直于 x x x l l l S L S_L S L S R S_R S R 治 :分别找出 S L S_L S L S R S_R S R 合 :对于 S L S_L S L p \mathbf{p} p p x \mathbf{p}_x p x S R S_R S R y \mathbf{y} y 据此可得到如下过程:
主定理 设 a ≥ 1 , b > 1 \textcolor{red}{a} \geq 1, \textcolor{green}{b} > 1 a ≥ 1 , b > 1 f ( n ) f(n) f ( n ) f ( n ) ∈ Θ ( n m ) f(n)\in \Theta(n^{\textcolor{blue}{m}}) f ( n ) ∈ Θ ( n m ) 阶数 ),T ( n ) T(n) T ( n )
T ( n ) = a T ( n b ) + Θ ( n m ) T(n) = \textcolor{red}{a} T(\frac{n}{\textcolor{green}{b}}) + \Theta(n^{\textcolor{blue}{m}}) T ( n ) = a T ( b n ) + Θ ( n m )
其中 a \textcolor{red}{a} a b \textcolor{green}{b} b 1 b \frac{1}{\textcolor{green}{b}} b 1 f ( n ) ∈ Θ ( n m ) f(n)\in \Theta(n^{\textcolor{blue}{m}}) f ( n ) ∈ Θ ( n m )
T ( n ) = { Θ ( n m ) log b a < m , 非递归成本占主导 Θ ( n m log n ) log b a = m , 平衡点 Θ ( n log b a ) log b a > m , 递归成本占主导 T(n)= \begin{cases} \Theta(n^{\textcolor{blue}{m}})&&\log_{\textcolor{green}{b}} \textcolor{red}{a}<{\textcolor{blue}{m}}, \text{非递归成本占主导}\\ \Theta(n^{\textcolor{blue}{m}} \log n)&&\log_{\textcolor{green}{b}} \textcolor{red}{a}={\textcolor{blue}{m}}, \text{平衡点}\\ \Theta(n^{\log_{\textcolor{green}{b}} \textcolor{red}{a}})&&\log_{\textcolor{green}{b}} \textcolor{red}{a}>{\textcolor{blue}{m}}, \text{递归成本占主导} \end{cases} T ( n ) = ⎩ ⎨ ⎧ Θ ( n m ) Θ ( n m log n ) Θ ( n l o g b a ) log b a < m , 非递归成本占主导 log b a = m , 平衡点 log b a > m , 递归成本占主导
或者:
T ( n ) = { Θ ( n max ( log b a , m ) ) log b a ≠ m Θ ( n m log n ) log b a = m \boxed{T(n)= \begin{cases} \Theta(n^{\max(\log_{\textcolor{green}{b}} \textcolor{red}{a}, {\textcolor{blue}{m}})})&&\log_{\textcolor{green}{b}} \textcolor{red}{a} \ne {\textcolor{blue}{m}}\\ \Theta(n^{\textcolor{blue}{m}} \log n)&&\log_{\textcolor{green}{b}} \textcolor{red}{a}={\textcolor{blue}{m}}\\ \end{cases}} T ( n ) = { Θ ( n m a x ( l o g b a , m ) ) Θ ( n m log n ) log b a = m log b a = m
注意:
子问题规模必须为 n b \frac{n}{\textcolor{green}{b}} b n f ( n ) f(n) f ( n ) f ( n ) = Θ ( n m ) f(n) = \Theta(n^{\textcolor{blue}{m}}) f ( n ) = Θ ( n m ) 即使在 n n n T ( n ) T(n) T ( n ) 主定理仍然是成立的 对 T ( n ) T(n) T ( n ) k k k k k k
T ( n ) = a k T ( n b k ) + ∑ i = 0 k − 1 a i f ( n b i ) T(n) = a^k T\left(\frac{n}{b^k}\right) + \sum_{i=0}^{k-1} a^i f\left(\frac{n}{b^i}\right) T ( n ) = a k T ( b k n ) + i = 0 ∑ k − 1 a i f ( b i n )
当 n b k = 1 \frac{n}{b^k} = 1 b k n = 1 k = log b n k = \log_b n k = log b n
T ( 1 ) = Θ ( 1 ) T(1) = \Theta(1) T ( 1 ) = Θ ( 1 )
于是得到完整的递归展开式:
T ( n ) = Θ ( n log b a ) + ∑ i = 0 log b n − 1 a i f ( n b i ) T(n) = \Theta(n^{\log_b a}) + \sum_{i=0}^{\log_b n - 1} a^i f\left(\frac{n}{b^i}\right) T ( n ) = Θ ( n l o g b a ) + i = 0 ∑ l o g b n − 1 a i f ( b i n )
其中 a k = a log b n = n log b a a^k = a^{\log_b n} = n^{\log_b a} a k = a l o g b n = n l o g b a
设 i ∈ [ 0 , log b n − 1 ] i \in [0, \log_b n - 1] i ∈ [ 0 , log b n − 1 ] n i = n b i n_i = \frac{n}{b^i} n i = b i n
T ( n ) = Θ ( n log b a ) + ∑ i = 0 log b n − 1 a i f ( n i ) T(n) = \Theta(n^{\log_b a}) + \sum_{i=0}^{\log_b n - 1} a^i f(n_i) T ( n ) = Θ ( n l o g b a ) + i = 0 ∑ l o g b n − 1 a i f ( n i )
记这个求和为:
S ( n ) = ∑ i = 0 log b n − 1 a i f ( n b i ) S(n) = \sum_{i=0}^{\log_b n - 1} a^i f\left(\frac{n}{b^i}\right) S ( n ) = i = 0 ∑ l o g b n − 1 a i f ( b i n )
这个求和项决定了整个递归的主导成本 ,我们将根据 f ( n ) f(n) f ( n ) n log b a n^{\log_b a} n l o g b a S ( n ) S(n) S ( n )
情形一 :
如果 f ( n ) = O ( n log b a − ϵ ) f(n) = O(n^{\log_b a - \epsilon}) f ( n ) = O ( n l o g b a − ϵ ) n log b a n^{\log_b a} n l o g b a
a i f ( n b i ) ≤ a i ⋅ C ⋅ ( n b i ) log b a − ϵ = C n log b a − ϵ ⋅ ( a b log b a − ϵ ) i a^i f\left(\frac{n}{b^i}\right) \leq a^i \cdot C \cdot \left(\frac{n}{b^i}\right)^{\log_b a - \epsilon} = C n^{\log_b a - \epsilon} \cdot \left(\frac{a}{b^{\log_b a - \epsilon}}\right)^i a i f ( b i n ) ≤ a i ⋅ C ⋅ ( b i n ) l o g b a − ϵ = C n l o g b a − ϵ ⋅ ( b l o g b a − ϵ a ) i
因为 a = b log b a a = b^{\log_b a} a = b l o g b a
a b log b a − ϵ = b ϵ > 1 \frac{a}{b^{\log_b a - \epsilon}} = b^{\epsilon} > 1 b l o g b a − ϵ a = b ϵ > 1
说明是一个等比数列 ,但总和仍是 O ( n log b a ) O(n^{\log_b a}) O ( n l o g b a )
T ( n ) = Θ ( n log b a ) T(n) = \Theta(n^{\log_b a}) T ( n ) = Θ ( n l o g b a )
情形二 :
如果 f ( n ) = Θ ( n log b a ) f(n) = \Theta(n^{\log_b a}) f ( n ) = Θ ( n l o g b a )
S ( n ) = ∑ i = 0 log b n − 1 a i ( n b i ) log b a = ∑ i = 0 log b n − 1 n log b a = Θ ( n log b a log n ) S(n) = \sum_{i=0}^{\log_b n - 1} a^i \left( \frac{n}{b^i} \right)^{\log_b a} = \sum_{i=0}^{\log_b n - 1} n^{\log_b a} = \Theta(n^{\log_b a} \log n) S ( n ) = i = 0 ∑ l o g b n − 1 a i ( b i n ) l o g b a = i = 0 ∑ l o g b n − 1 n l o g b a = Θ ( n l o g b a log n )
于是:
T ( n ) = Θ ( n log b a log n ) T(n) = \Theta(n^{\log_b a} \log n) T ( n ) = Θ ( n l o g b a log n )
情形三 :
如果 f ( n ) = Ω ( n log b a + ϵ ) f(n) = \Omega(n^{\log_b a + \epsilon}) f ( n ) = Ω ( n l o g b a + ϵ ) 正则性条件 :
∃ c < 1 , 使得 a f ( n b ) ≤ c f ( n ) \exists c < 1, \text{使得} \quad a f\left(\frac{n}{b}\right) \leq c f(n) ∃ c < 1 , 使得 a f ( b n ) ≤ c f ( n )
那么可以证明 S ( n ) = Θ ( f ( n ) ) S(n) = \Theta(f(n)) S ( n ) = Θ ( f ( n ))
T ( n ) = Θ ( f ( n ) ) T(n) = \Theta(f(n)) T ( n ) = Θ ( f ( n ))
贪心 贪心法适用于这样的优化问题 :
输入 :有 n n n 目标 :从中选出一个子集 ,使它在满足某些约束条件 的前提下,目标函数最优(最大或最小)贪心法的核心思路是:每一步都做出当前看来最优的选择 ,希望通过一系列局部最优来得到全局最优:
选标准 :根据目标函数定义一个“优先选择”的量度标准逐个选择输入 :在未处理的输入中,按标准选一个当前最优的元素(局部最优)判断能不能加 :如果当前这个元素加到部分解中后还满足约束,就加进去重复直到结束 贪心法只是局部最优策略 ,它不回溯、不考虑整体,某一步选的局部最优可能错失了全局最优。所以它并不一定能得到最优解。贪心法的核心难点是选一个“可保证最优”的量度标准 。
1 2 3 4 5 6 7 Procedure GREEDY(A, n)
SELECT: 按贪心标准从输入中选最优FEASIBLE: 检查当前加入是否违背约束UNION: 加入解中并更新状态贪心法的优点 有:
简单、直观 时间效率高,常是线性或近线性 在某些问题上确实能得最优解 缺点 是:
不是所有问题都适用 量度标准不一定存在 或不好找必须通过数学证明该标准能保证最优解 小数背包 给你 n n n
目标 :选择一组 x i x_i x i
约束条件 :总重量 ∑ w i x i ≤ M \sum w_i x_i \le M ∑ w i x i ≤ M
目标函数 :总价值 ∑ p i x i \sum p_i x_i ∑ p i x i
按性价比 p i / w i p_i/w_i p i / w i 依次从头开始装入背包:
如果能装满当前整个物品(还剩空间 ≥ 当前物品重量),就全装进去; 否则装一部分,正好填满剩余空间,之后退出 这个策略每次都选择“当前最划算”的物品(单位重量价值最大),符合贪心思想。
1 2 3 4 5 6 7 8 9 GREEDY-KNAPSACK(P, W, M, X, n):
时间复杂度 :
排序阶段:O ( n log n ) O(n \log n) O ( n log n ) 主循环阶段:最多遍历 n n n O ( n ) O(n) O ( n ) 定理 :如果 p 1 / w 1 ≥ p 2 / w 2 ≥ … ≥ p n / w n p_1/w_1 \ge p_2/w_2 \ge\ldots \ge p_n/w_n p 1 / w 1 ≥ p 2 / w 2 ≥ … ≥ p n / w n GREEDY-KNAPSACK 对于给定的背包问题实例生成一个最优解。
可以通过构造法证明 :贪心算法得到的解 X X X Y Y Y Y Y Y X X X 并且总价值不变或变大 。
假设 :
贪心解 为 X = ( x 1 , … , x n ) X = (x_1, \dots, x_n) X = ( x 1 , … , x n ) 有一个最优解 Y = ( y 1 , … , y n ) Y = (y_1, \dots, y_n) Y = ( y 1 , … , y n ) X X X ∑ p i y i > ∑ p i x i \sum p_i y_i > \sum p_i x_i ∑ p i y i > ∑ p i x i 但这是不可能的:
贪心算法会按单位价值从高到低装满物品。
假设 X X X Y Y Y 第一个不一样的地方 是第 k k k
对于前 k − 1 k-1 k − 1 x i = y i = 1 x_i = y_i = 1 x i = y i = 1 第 k k k x k x_k x k Y Y Y X X X y k < x k y_k < x_k y k < x k 因为背包总容量一样,可以从 Y Y Y x k > y k x_k > y_k x k > y k k + 1 k+1 k + 1 n n n k k k
这样构造一个新解 Z Z Z
总容量仍为 M M M 总价值 ∑ p i z i ≥ ∑ p i y i \sum p_i z_i \ge \sum p_i y_i ∑ p i z i ≥ ∑ p i y i 重复上述操作,最终将 Y Y Y X X X X X X
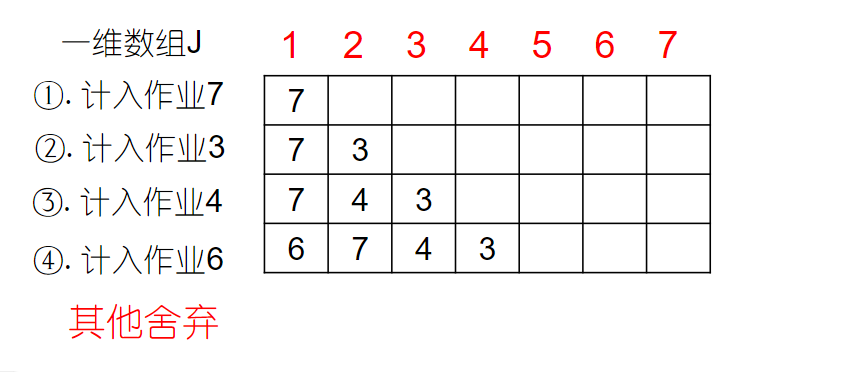
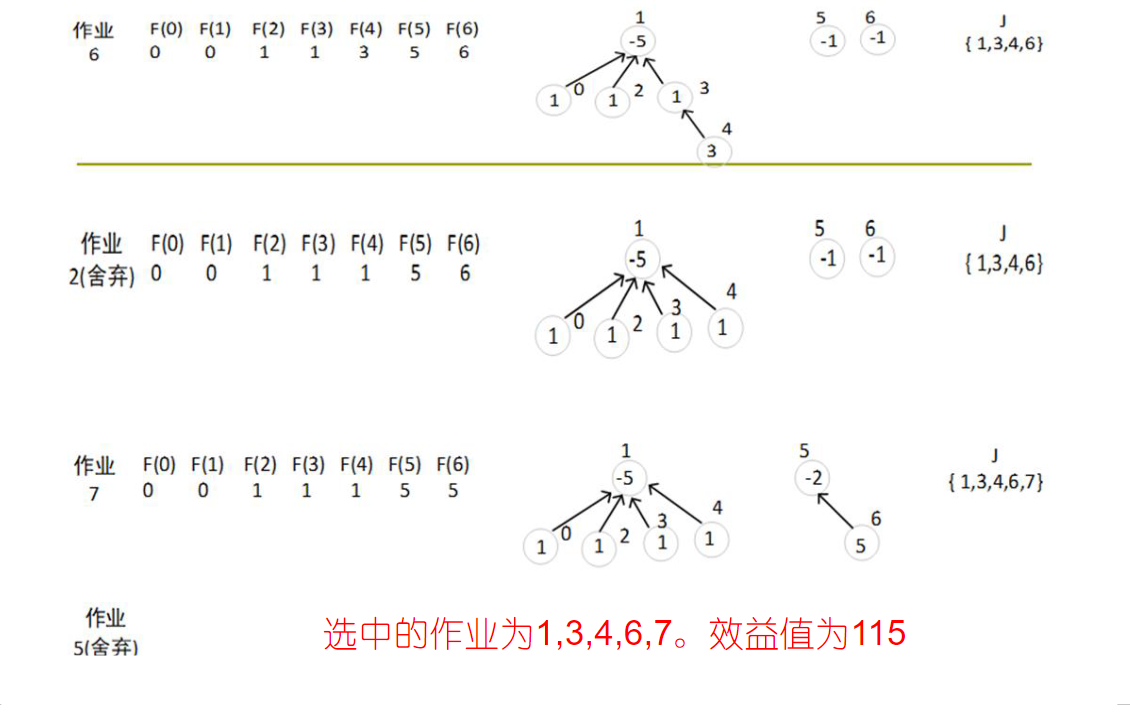
作业调度问题 有一台机器(每次只能处理一个作业)和 n n n
只能运行 1 个单位时间 ; 有一个截止时间 d i d_i d i d i d_i d i 若在截止前完成,就可以获得 利润 p i > 0 p_i > 0 p i > 0 ,否则利润为 0。 从 n n n 使总利润最大 。
优先选择利润最大的作业 ,然后尽可能安排一个时间片让它完成,且在不违反其他作业截止时间的前提下。
1 2 3 4 5 6 按 p_i 降序排列作业;
证明这个方式是最优的 ,需要构造两个解:
J J J I I I 假设 J ≠ I J \neq I J = I a ∈ J a \in J a ∈ J a ∉ I a \notin I a ∈ / I J J J a a a 收益最大 的那个。
贪心选择作业 a a a b ∈ I ∖ J b \in I \setminus J b ∈ I ∖ J
p a ≥ p b p_a \ge p_b p a ≥ p b
因为如果存在某个 b b b a a a p b > p a p_b > p_a p b > p a b b b a a a
设:
S I S_I S I I I I S J S_J S J J J J 将两个调度表相同的作业放在相同的时间片执行:
我们用 a a a I I I b b b a a a
I ′ = I ∖ { b } ∪ { a } I' = I \setminus \{b\} \cup \{a\} I ′ = I ∖ { b } ∪ { a }
此时:
由于 p a ≥ p b p_a \ge p_b p a ≥ p b 由于时间槽合法(因为 J J J I ′ I' I ′ J J J 重复替换 ,直至 I I I J J J
收益 ( J ) ≥ 收益 ( I ) \text{收益}(J) \ge \text{收益}(I) 收益 ( J ) ≥ 收益 ( I )
所以 J J J
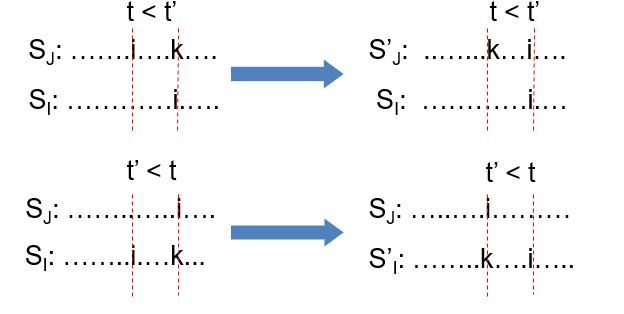
定理 ,判断排列是否可行 :对于作业集合 J = { i 1 , i 2 , … , i k } J = \{i_1, i_2, \dots, i_k\} J = { i 1 , i 2 , … , i k } d i 1 ≤ d i 2 ≤ ⋯ ≤ d i k d_{i_1} \leq d_{i_2} \leq \cdots \leq d_{i_k} d i 1 ≤ d i 2 ≤ ⋯ ≤ d i k
如果按照这个顺序安排这些作业,且所有作业在其截止时间前完成,那么这个集合是可行解 ; 反过来 ,如果集合 J J J 即:作业集合 J J J 当且仅当 这些作业可以按照 σ \sigma σ
在判断一个作业集合是否可行 时,其实不用把所有排列都试一遍,只需要验证一个非常特殊的顺序就可以了 ——按截止时间升序安排 (按 d i d_i d i
证明 :
换句话说:我们每次交换时,是让一个更早截止的作业向前,保证排序越来越接近 σ \sigma σ
graph TD
A["初始可行顺序 σ' = (r1, r2, ..., ra, ..., rb, ..., rk)"] --> B["找到第一个位置a,使ra ≠ ia"]
B --> C["在σ'中找到rb = ia,且 b > a"]
C --> D["交换 ra 和 rb 得到 σ'' "]
D --> E["σ'' 仍然是可行顺序"]
E --> F["σ'' == σ?"]
F -- "是" --> G["转换完成,得到了按截止时间升序的 σ"]
F -- "否" --> H["将σ''作为新的σ',重复交换过程"]
H --> B
运用上面的定理,就可以检验序列是否可行 。
假设当前已经选了 J ( 1 ) , J ( 2 ) , … , J ( k ) J(1), J(2), \dots, J(k) J ( 1 ) , J ( 2 ) , … , J ( k ) 截止时间 满足:
D [ J ( 1 ) ] ≤ D [ J ( 2 ) ] ≤ ⋯ ≤ D [ J ( k ) ] D[J(1)] \leq D[J(2)] \leq \cdots \leq D[J(k)] D [ J ( 1 )] ≤ D [ J ( 2 )] ≤ ⋯ ≤ D [ J ( k )]
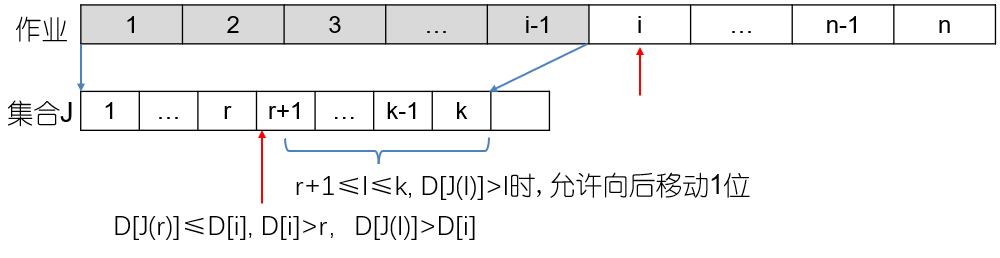
现在来了一个新作业 i i i J J J J J J
按截止时间升序排列 ;每个作业的执行时间 ≤ 它的截止时间 要将作业 i i i r + 1 r+1 r + 1 l > r l>r l > r D [ J ( l ) ] ≥ l D[J(l)] \geq l D [ J ( l )] ≥ l r + 1 r+1 r + 1 k k k
直接插入法求解 :
将所有作业按收益 p j p_j p j 从大到小排序 ; 依次考虑每个作业,尝试安排在 不晚于它截止时间的最晚空闲时间点 ;尝试找到一个位置 r r r i i i r + 1 r+1 r + 1 把作业 i i i r + 1 r+1 r + 1 r + 1 r+1 r + 1 如果存在这样的时间点,就安排作业;否则跳过。 gantt
dateFormat x
section 作业
作业1 :a1, 0, 1
作业3 :a3, 1, 1
尝试插入作业 i = 5 i=5 i = 5 D [ 5 ] = 2 D[5]=2 D [ 5 ] = 2
我们向前找,发现 J [ 2 ] = 3 J[2]=3 J [ 2 ] = 3 D [ 3 ] > D [ 5 ] D[3]>D[5] D [ 3 ] > D [ 5 ]
再往前找,J [ 1 ] = 1 J[1]=1 J [ 1 ] = 1 D [ 1 ] ≤ D [ 5 ] D[1]≤D[5] D [ 1 ] ≤ D [ 5 ] J [ 1 ] J[1] J [ 1 ]
gantt
dateFormat x
section 作业
作业1 :a1, 0, 1
作业5 :a5, 1, 1
作业3 :a3, 2, 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 #include <iostream> #include <vector> using namespace std;int JS (const vector<int >& D, vector<int >& J) int n = D.size () - 1 ; 0 ] = 0 ; 1 ] = 1 ; int k = 1 ; for (int i = 2 ; i <= n; ++i) {int r = k;while (D[J[r]] > D[i] && D[J[r]] != r) {if (D[J[r]] <= D[i] && D[i] > r) {for (int l = k; l >= r + 1 ; --l) {1 ] = J[l];1 ] = i;return k;
时间复杂度为 O ( n 2 ) O(n^2) O ( n 2 )
n = 7 n=7 n = 7 ( p 1 , … , p 7 ) = ( 3 , 5 , 20 , 18 , 1 , 6 , 30 ) (p_1,\dots,p7)=(3,5,20,18,1,6,30) ( p 1 , … , p 7 ) = ( 3 , 5 , 20 , 18 , 1 , 6 , 30 ) ( d 1 , … , d 7 ) = ( 1 , 3 , 4 , 3 , 2 , 1 , 2 ) (d_1,\dots,d7)=(1,3,4,3,2,1,2) ( d 1 , … , d 7 ) = ( 1 , 3 , 4 , 3 , 2 , 1 , 2 ) 按照 p p p
( p 7 , p 3 , p 4 , p 6 , p 2 , p 1 , p 5 ) = ( 30 , 20 , 18 , 6 , 5 , 3 , 1 ) (p_7, p_3, p_4, p_6, p_2, p_1, p_5)=(30,20,18,6,5,3,1) ( p 7 , p 3 , p 4 , p 6 , p 2 , p 1 , p 5 ) = ( 30 , 20 , 18 , 6 , 5 , 3 , 1 )
对应期限为 ( 2 , 4 , 3 , 1 , 3 , 1 , 2 ) (2, 4, 3, 1, 3, 1, 2) ( 2 , 4 , 3 , 1 , 3 , 1 , 2 )
按这个顺序安排即可。
可以用并查集 优化上面的算法,即让每个时间片 t t t 当前最晚的可用时间点 。
对于一个作业,其截止时间是 d d d
使用 FIND(t) 找出最晚的空闲时间点 如果这个时间点 t t t t t t t t t t − 1 t-1 t − 1 t t t t − 1 t-1 t − 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 #include <iostream> #include <vector> using namespace std;int FIND (vector<int >& P, int x) if (P[x] < 0 ) return x;return P[x] = FIND (P, P[x]);void UNION (vector<int >& P, int i, int j) if (P[i] < P[j]) {else {int FJS (const vector<int >& D, vector<int >& J) int n = D.size () - 1 ;int b = 0 ;for (int i = 1 ; i <= n; ++i)max (b, D[i]);min (n, b); vector<int > F (b + 1 ) , P (b + 1 ) ;for (int i = 0 ; i <= b; ++i) {-1 ;int k = 0 ;for (int i = 1 ; i <= n; ++i) {int j = FIND (P, min (n, D[i]));if (F[j] != 0 ) {int l = FIND (P, F[j] - 1 );UNION (P, l, j);return k;
时间复杂度分析:
排序: O ( n log n ) O(n \log n) O ( n log n ) 并查集的 find 和 union: O ( α ( n ) ) ≈ O ( 1 ) O(\alpha(n))\approx O(1) O ( α ( n )) ≈ O ( 1 ) 总时间复杂度 O ( n log n ) O(n \log n) O ( n log n )
n = 7 n=7 n = 7 ( p 1 , p 2 , … , p 7 ) = ( 40 , 12 , 30 , 20 , 7 , 15 , 10 ) (p_1,p_2,\dots,p_7)=(40, 12, 30, 20, 7, 15, 10) ( p 1 , p 2 , … , p 7 ) = ( 40 , 12 , 30 , 20 , 7 , 15 , 10 ) ( d 1 , d 2 , … , d 7 ) = ( 2 , 4 , 4 , 3 , 2 , 1 , 6 ) (d_1,d_2,\dots,d_7)=(2, 4, 4, 3, 2, 1, 6) ( d 1 , d 2 , … , d 7 ) = ( 2 , 4 , 4 , 3 , 2 , 1 , 6 ) 按 p p p
( p 1 , p 3 , p 4 , p 6 , p 2 , p 7 , p 5 ) = ( 40 , 30 , 20 , 15 , 12 , 10 , 7 ) (p_1, p_3, p_4, p_6, p_2, p_7, p_5)=(40, 30, 20, 15, 12, 10 , 7) ( p 1 , p 3 , p 4 , p 6 , p 2 , p 7 , p 5 ) = ( 40 , 30 , 20 , 15 , 12 , 10 , 7 ) 对应的期限为 ( 2 , 4 , 3 , 1 , 4 , 6 , 2 ) (2, 4, 3, 1, 4, 6, 2) ( 2 , 4 , 3 , 1 , 4 , 6 , 2 ) b = min { n , max { d ( i ) } } = min { 7 , 6 } = 6 b = \min\{ n, \max\{d(i)\} \} = \min\{7, 6\}= 6 b = min { n , max { d ( i )}} = min { 7 , 6 } = 6
这个图画错了,看并查集数组的值。
区间选取问题 是作业调度问题的变式,给定若干个开区间 ( a , b ) (a, b) ( a , b )
按区间的右端点(即 b b b
复杂度 O ( n log n ) O(n\log n) O ( n log n )
最小生成树问题 最小生成树 (MST) 问题定义如下:
原始图 :
图 G = ( V , E ) G=(V,E) G = ( V , E ) 加权无向连通图 。
顶点集 V V V E E E
每条边 e ∈ E e\in E e ∈ E w ( e ) w(e) w ( e )
生成树 :
从原图中取部分边形成的树 T = ( V , E ′ ) T=(V,E') T = ( V , E ′ )
T T T ∣ V ∣ |V| ∣ V ∣ n − 1 n-1 n − 1
最小生成树就是在所有可能的生成树中,总边权和最小 的那一棵树。
权值从小到大排列 就是最优量度标准:因为如果跳过了更小的边,那就会用更大的边连接某些连通分支,造成全局代价上升。
初始化一个空边集 T = ∅ T = \emptyset T = ∅
将所有边按照权重从小到大排序 。
从边数看,复杂度 O ( e log e ) O(e \log e) O ( e log e ) 从点数看,复杂度 e ≤ n ( n − 1 ) / 2 ⇒ O ( n 2 log n ) e\le n(n-1)/2 \Rightarrow O(n^2\log n) e ≤ n ( n − 1 ) /2 ⇒ O ( n 2 log n ) 依次取权值最小的边 ( u , v ) (u,v) ( u , v )
如果这条边不会使得 T T T 判环用并查集 判点,路径压缩+按秩合并复杂度大致为 O ( α ( n ) ) O(\alpha(n)) O ( α ( n )) 重复,直到 T T T n − 1 n-1 n − 1
总复杂度近似 O ( e log e ) O(e \log e) O ( e log e )
证明 : Kruskal 算法构造出的生成树 T T T 交换法 + 反证法 。
假设 T T T T ′ T' T ′ 若 T ≠ T ′ T ≠ T' T = T ′ e ∈ T e \in T e ∈ T e ∉ T ′ e \notin T' e ∈ / T ′ 把 e e e T ′ T' T ′ T ′ T' T ′ 在这个环中,必定存在一条边 e j ∈ T ′ e_j \in T' e j ∈ T ′ e j ∉ T e_j \notin T e j ∈ / T 如果 e j e_j e j e e e e j e_j e j e e e 所以 c ( e j ) ≥ c ( e ) c(e_j) ≥ c(e) c ( e j ) ≥ c ( e ) e j e_j e j e e e T ′ ′ T'' T ′′ T ′ T' T ′ 重复这个过程,最终可以把 T ′ T' T ′ T T T T T T 旅行商问题的贪心解法 旅行商问题 (TSP) 即:给定一组城市以及任意两城市之间的距离(或代价),一位售货员需要:
从一个城市出发; 每个城市恰好访问一次; 最后回到出发城市; 使得路径总和最短 。本质是一个最短哈密顿回路 问题,属于 NP 完全问题 。
当前在城市 i; 选择距离 i 最近、尚未访问 的城市 j; 重复这个过程,直到所有城市访问一次; 最后返回起点城市。 总体复杂度 O ( n 2 ) O(n^2) O ( n 2 )
贪心法在 TSP 问题中,得到的是一个次优解 。
动态规划 动态规划适用于 多阶段决策优化问题 ,这类问题一般具有如下几个特点:
多阶段性 :问题可以被划分为多个阶段,每个阶段需要做一个决策。
每阶段的状态只依赖前一阶段 :也就是说,第 i i i i − 1 i-1 i − 1 不依赖于更早的阶段 ,这点是和回溯的区别。
存在重叠子问题 :问题的子结构重复出现,所以可以用数组或表格把中间结果存下来,避免重复计算。
子问题的最优解能构成原问题的最优解 ,也就是最优性原理。这是一定满足的 。
动态规划的设计核心是这几个步骤:
确定阶段、状态和决策:当前所处的情形 ,可以做出的选择 。 设计递推关系式 (状态转移方程)。 确定初始状态和边界条件 。 迭代方法自底向上求解 。 动态规划一般采用的就是迭代方法,因为递归时间空间复杂度都很高,会重复计算子问题;而迭代采用数组保存数据,不会导致子问题重复计算,比递归快很多。
最优性原理 如果一个问题的最优解包含了它的子问题的最优解,那么这个问题就满足最优性原理 。
也就是说最优解可以通过子问题的最优解一步步构建出来 。
如果一个问题的子问题不包含最优解,则原问题不满足最优性原理。
如果要证明一个问题可以用动态规划解,一般需要就证明它满足最优性原理:
写出原问题的最优解形式
比如:最优路径 = 从起点到 A 的最优路径 + 从 A 到终点的最优路径 设定初始状态和初始决策
分析初始决策后的状态变化
比如:从点 1 走向点 2,剩下的问题是从点 2 到终点 证明后续路径必须是该子问题的最优解
辨析 :任意子问题的最优决策序列,都是原问题的部分最优解吗?
只有原问题的最优解所用到的那些子问题 ,它们的最优解才是原问题的“部分最优解”。
不满足最优性原理的例子 :
若多段图问题,以乘法为路径长度,当含有负权时,全局最优解不依赖于子问题的最优解 ,最优性原理不成立; 包含负长度环的任意两点间最短路径问题 ,最优性原理也不成立。 0/1 背包问题 n n n p i p_i p i w i w_i w i 一个背包,最大容量为 M M M 每个物品只能 选或不选 ,不能选一半 即在满足 ∑ w i x i ≤ M \sum w_i x_i \leq M ∑ w i x i ≤ M x i ∈ { 0 , 1 } x_i \in \{0,1\} x i ∈ { 0 , 1 } ∑ p i x i \sum p_i x_i ∑ p i x i
用 KNAP ( i , j , X ) \text{KNAP}(i,j,X) KNAP ( i , j , X ) KNAP ( 1 , n , M ) \text{KNAP}(1,n,M) KNAP ( 1 , n , M )
用贪心法是得不到最优解的 。
n = 3 , M = 6 , ( p 1 , p 2 , p 3 ) = ( 3 , 4 , 8 ) , ( w 1 , w 2 , w 3 ) = ( 1 , 2 , 5 ) n=3, M=6, (p_1,p_2,p_3)=(3,4,8),(w_1,w_2,w_3)=(1,2,5) n = 3 , M = 6 , ( p 1 , p 2 , p 3 ) = ( 3 , 4 , 8 ) , ( w 1 , w 2 , w 3 ) = ( 1 , 2 , 5 ) p i / w i p_i/w_i p i / w i
( p 1 / w 1 , p 2 / w 2 , p 3 / w 3 ) = ( 3 , 2 , 1.6 ) (p_1/w_1,p_2/w_2,p_3/w_3)=(3,2,1.6) ( p 1 / w 1 , p 2 / w 2 , p 3 / w 3 ) = ( 3 , 2 , 1.6 )
其解是 ( 1 , 1 , 0 ) (1, 1, 0) ( 1 , 1 , 0 ) ( 1 , 0 , 1 ) (1, 0, 1) ( 1 , 0 , 1 )
更简单的例子 :
M = 5 , { ( p , w ) } = { ( 5 , 5 ) , ( 2 , 1 ) , ( 2 , 1 ) } M=5, \{(p, w)\}=\{(5, 5), (2, 1), (2, 1)\} M = 5 , {( p , w )} = {( 5 , 5 ) , ( 2 , 1 ) , ( 2 , 1 )}
用贪心法得到的解是 ( 0 , 1 , 1 ) (0, 1, 1) ( 0 , 1 , 1 ) ( 1 , 0 , 0 ) (1, 0, 0) ( 1 , 0 , 0 )
问题的最优性原理 :
假设物品序列 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x 1 , x 2 , … , x n
如果 x 1 = 0 x_1 = 0 x 1 = 0 KNAP ( 2 , n , M ) \text{KNAP}(2,n,M) KNAP ( 2 , n , M ) 且必须最优
如果 x 1 = 1 x_1 = 1 x 1 = 1 KNAP ( 2 , n , M − w 1 ) \text{KNAP}(2,n,M-w_1) KNAP ( 2 , n , M − w 1 ) 且必须最优
如果后面不是用最优方案,那整个结果就会比用子问题最优解来得差。毕竟在 0/1 背包问题里面,要得到的效益是两个子问题直接加起来组合起来的,要注意其他问题不一定是这样。
即满足最优解的一部分子问题也必须是最优的,说明可以用动态规划来解决。
向后处理法 从前往后。
设 f [ i ] [ j ] f[i][j] f [ i ] [ j ] i i i j j j
状态转移方程为:
f [ i ] [ j ] = { f [ i − 1 ] [ j ] 不选第 i 个物品 f [ i − 1 ] [ j − w i ] + p i 选第 i 个物品 f[i][j] = \begin{cases} f[i-1][j] & \text{不选第 } i \text{ 个物品} \\ f[i-1][j - w_i] + p_i & \text{选第 } i \text{ 个物品} \\ \end{cases} f [ i ] [ j ] = { f [ i − 1 ] [ j ] f [ i − 1 ] [ j − w i ] + p i 不选第 i 个物品 选第 i 个物品
即:
f [ i ] [ j ] = max ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − w i ] + p i ) f[i][j] = \max\left( f[i-1][j],\ f[i-1][j - w_i] + p_i \right) f [ i ] [ j ] = max ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − w i ] + p i )
边界条件:
f [ 0 ] [ j ] = 0 f[0][j] = 0 f [ 0 ] [ j ] = 0 1 2 3 4 5 6 7 8 9 10 11 12 def knapsack_01 (weights, values, M ):len (weights)0 ] * (M + 1 ) for _ in range (n + 1 )]for i in range (1 , n + 1 ): for j in range (M + 1 ): if j >= weights[i - 1 ]:max (dp[i-1 ][j], dp[i-1 ][j - weights[i-1 ]] + values[i-1 ])else :1 ][j]return dp[n][M]
可以看到状态转移方程只有第二维影响结果 ,所以可以简化为:
f [ j ] = max ( f [ j ] , f [ j − w i ] + p i ) f[j] = \max\left( f[j],\ f[j - w_i] + p_i \right) f [ j ] = max ( f [ j ] , f [ j − w i ] + p i )
向前处理法 从后往前,理论上可行,但编程不常用。
向前处理强调:j + 1 j+1 j + 1 g j ( X ) = KNAP ( j + 1 , n , X ) g_j(X) = \text{KNAP}(j+1, n, X) g j ( X ) = KNAP ( j + 1 , n , X )
推导形式为:
g j ( X ) = max ( g j + 1 ( X ) , g j + 1 ( X − w j + 1 ) + p j + 1 ) g_j(X) = \max(g_{j+1}(X),\ g_{j+1}(X - w_{j+1}) + p_{j+1}) g j ( X ) = max ( g j + 1 ( X ) , g j + 1 ( X − w j + 1 ) + p j + 1 )
这个其实和向后处理是对称的,只是方向相反,主要用于理论推导。
时间复杂度 O ( n M ) O(nM) O ( n M )
空间复杂度 O ( n M ) → O ( M ) O(nM)\to O(M) O ( n M ) → O ( M ) O ( n M ) O(nM) O ( n M )
1 2 3 4 5 6 7 8 9 10 11 int w = W;int > selected_items;for (int i = n; i >= 1 ; --i) if (dp[i][w] != dp[i - 1 ][w]) push_back (i - 1 ); 1 ].weight;
序偶对法解法 序偶对法的核心思想是迭代地构建一个集合,集合中的元素是 (效益 , 重量) 序偶对。在每一步迭代中,考虑是否将当前物品放入背包,并根据一定的规则(支配规则、容量限制)来更新和筛选这些序偶对。
( p i , w i ) (p_i, w_i) ( p i , w i ) i i i M M M 序偶对 : 表示为 ( P , W ) (P, W) ( P , W ) P P P W W W 集合的定义
S i − 1 S^{i-1} S i − 1 i − 1 i-1 i − 1 所有满足约束条件且非支配的 序偶对 ( P , W ) (P, W) ( P , W ) f i − 1 f_{i-1} f i − 1
S 1 i S^i_1 S 1 i S i − 1 S^{i-1} S i − 1 i i i ( p i , w i ) (p_i, w_i) ( p i , w i ) S i − 1 S^{i-1} S i − 1 每一个可能的序偶对 后形成的新序偶对的集合。
具体地,如果 ( P ′ , W ′ ) ∈ S i − 1 (P', W') \in S^{i-1} ( P ′ , W ′ ) ∈ S i − 1 i i i ( P ′ + p i , W ′ + w i ) (P'+p_i, W'+w_i) ( P ′ + p i , W ′ + w i ) S 1 i = { ( P , W ) ∣ ( P − p i , W − w i ) ∈ S i − 1 and W ≤ M } S^i_1 = \{ (P,W) | (P-p_i, W-w_i) \in S^{i-1} \text{ and } W \le M \} S 1 i = {( P , W ) ∣ ( P − p i , W − w i ) ∈ S i − 1 and W ≤ M } 简单来说,就是将 ( p i , w i ) (p_i, w_i) ( p i , w i ) S i − 1 S^{i-1} S i − 1 M M M S i S^i S i i i i S i − 1 S^{i-1} S i − 1 i i i S 1 i S^i_1 S 1 i i i i 支配规则 (选性价比更好的)和容量约束 。
支配规则用于去除那些肯定不会导致最优解的序偶对 ,从而减少计算量。例如,已知两个序偶对 ( P j , W j ) (P_j, W_j) ( P j , W j ) ( P k , W k ) (P_k, W_k) ( P k , W k ) W j ≥ W k W_j \ge W_k W j ≥ W k 且 P j ≤ P k P_j \le P_k P j ≤ P k ( P k , W k ) (P_k, W_k) ( P k , W k ) 支配 ( P j , W j ) (P_j, W_j) ( P j , W j ) ( P k , W k ) (P_k, W_k) ( P k , W k ) 更少(或相等)的重量获得了更高(或相等)的效益 ,因此 ( P j , W j ) (P_j, W_j) ( P j , W j )
在归并 S i − 1 S^{i-1} S i − 1 S 1 i S^i_1 S 1 i S i S^i S i
在生成 S i S^i S i S 1 i S^i_1 S 1 i W > M W > M W > M ( P , W ) (P,W) ( P , W ) 容量限制 。
算法的具体步骤是:
初始化 : S 0 = { ( 0 , 0 ) } S^0 = \{(0,0)\} S 0 = {( 0 , 0 )} 0 0 0 0 0 0
迭代 : 对于 i = 1 , 2 , … , n i = 1, 2, \dots, n i = 1 , 2 , … , n
生成 S 1 i S^i_1 S 1 i : S 1 i = { ( p ′ , w ′ ) ∣ ( p ′ − p i , w ′ − w i ) ∈ S i − 1 and w ′ ≤ M } S^i_1 = \{ (p',w') | (p'-p_i, w'-w_i) \in S^{i-1} \text{ and } w' \le M \} S 1 i = {( p ′ , w ′ ) ∣ ( p ′ − p i , w ′ − w i ) ∈ S i − 1 and w ′ ≤ M } S i − 1 S^{i-1} S i − 1 ( P , W ) (P,W) ( P , W ) W + w i ≤ M W+w_i \le M W + w i ≤ M ( P + p i , W + w i ) (P+p_i, W+w_i) ( P + p i , W + w i ) S 1 i S^i_1 S 1 i 归并生成 S i S^i S i : 将 S i − 1 S^{i-1} S i − 1 S 1 i S^i_1 S 1 i 去除 S 1 i S^i_1 S 1 i S i − 1 S^{i-1} S i − 1 去除 S i − 1 S^{i-1} S i − 1 S 1 i S^i_1 S 1 i 去除合并后集合内部互相支配的序偶。 确保所有序偶的重量 W ≤ M W \le M W ≤ M S i S^i S i 最优解 : S n S^n S n 效益值 P P P ,其 P P P S n S^n S n
如果需要确定决策序列 (回溯),即为了找出哪些物品被选中,需要从 S n S^n S n ( P ∗ , W ∗ ) (P^*, W^*) ( P ∗ , W ∗ )
对于第 n n n 如果 ( P ∗ , W ∗ ) ∈ S n − 1 (P^*, W^*) \in S^{n-1} ( P ∗ , W ∗ ) ∈ S n − 1 n n n x n = 0 x_n=0 x n = 0 n n n S n − 1 S^{n-1} S n − 1 ( P ∗ , W ∗ ) (P^*, W^*) ( P ∗ , W ∗ ) 如果 ( P ∗ , W ∗ ) ∉ S n − 1 (P^*, W^*) \notin S^{n-1} ( P ∗ , W ∗ ) ∈ / S n − 1 ( P ∗ − p n , W ∗ − w n ) ∈ S n − 1 (P^*-p_n, W^*-w_n) \in S^{n-1} ( P ∗ − p n , W ∗ − w n ) ∈ S n − 1 x n = 1 x_n=1 x n = 1 n n n S n − 1 S^{n-1} S n − 1 ( P ∗ − p n , W ∗ − w n ) (P^*-p_n, W^*-w_n) ( P ∗ − p n , W ∗ − w n ) 依此类推,从 S k S^{k} S k x k x_k x k S k − 1 S^{k-1} S k − 1 S 0 S^0 S 0 n = 3 n=3 n = 3 ( p 1 , p 2 , p 3 ) = ( 1 , 2 , 5 ) (p_1,p_2,p_3)=(1,2,5) ( p 1 , p 2 , p 3 ) = ( 1 , 2 , 5 ) ( w 1 , w 2 , w 3 ) = ( 2 , 3 , 4 ) (w_1,w_2,w_3)=(2,3,4) ( w 1 , w 2 , w 3 ) = ( 2 , 3 , 4 ) M = 6 M=6 M = 6
S 0 = { ( 0 , 0 ) } S^0 = \{(0,0)\} S 0 = {( 0 , 0 )}
i = 1 i=1 i = 1 ( p 1 , w 1 ) = ( 1 , 2 ) (p_1,w_1)=(1,2) ( p 1 , w 1 ) = ( 1 , 2 )
S 0 = { ( 0 , 0 ) } S^0 = \{(0,0)\} S 0 = {( 0 , 0 )} S 1 1 = { ( 0 + 1 , 0 + 2 ) } = { ( 1 , 2 ) } S^1_1 = \{(0+1, 0+2)\} = \{(1,2)\} S 1 1 = {( 0 + 1 , 0 + 2 )} = {( 1 , 2 )} 2 ≤ 6 2 \le 6 2 ≤ 6 S 1 = merge ( S 0 , S 1 1 ) = merge ( { ( 0 , 0 ) } , { ( 1 , 2 ) } ) S^1 = \text{merge}(S^0, S^1_1) = \text{merge}(\{(0,0)\}, \{(1,2)\}) S 1 = merge ( S 0 , S 1 1 ) = merge ({( 0 , 0 )} , {( 1 , 2 )}) ( 0 , 0 ) (0,0) ( 0 , 0 ) ( 1 , 2 ) (1,2) ( 1 , 2 ) W 0 = 0 ≱ W 1 = 2 W_0=0 \not\ge W_1=2 W 0 = 0 ≥ W 1 = 2 W 1 = 2 ≥ W 0 = 0 W_1=2 \ge W_0=0 W 1 = 2 ≥ W 0 = 0 P 1 = 1 ≥ P 0 = 0 P_1=1 \ge P_0=0 P 1 = 1 ≥ P 0 = 0 ( 1 , 2 ) (1,2) ( 1 , 2 ) ( 0 , 0 ) (0,0) ( 0 , 0 ) W 0 ≠ W 1 W_0 \neq W_1 W 0 = W 1 P 1 P 0 P_1 P_0 P 1 P 0 W 1 < W 0 W_1 < W_0 W 1 < W 0 S 1 = { ( 0 , 0 ) , ( 1 , 2 ) } S^1 = \{(0,0), (1,2)\} S 1 = {( 0 , 0 ) , ( 1 , 2 )} i = 2 i=2 i = 2 ( p 2 , w 2 ) = ( 2 , 3 ) (p_2,w_2)=(2,3) ( p 2 , w 2 ) = ( 2 , 3 )
S 1 = { ( 0 , 0 ) , ( 1 , 2 ) } S^1 = \{(0,0), (1,2)\} S 1 = {( 0 , 0 ) , ( 1 , 2 )}
S 1 2 S^2_1 S 1 2 从 ( 0 , 0 ) ∈ S 1 (0,0) \in S^1 ( 0 , 0 ) ∈ S 1 ( 0 + 2 , 0 + 3 ) = ( 2 , 3 ) (0+2, 0+3) = (2,3) ( 0 + 2 , 0 + 3 ) = ( 2 , 3 ) 3 ≤ 6 3 \le 6 3 ≤ 6 从 ( 1 , 2 ) ∈ S 1 (1,2) \in S^1 ( 1 , 2 ) ∈ S 1 ( 1 + 2 , 2 + 3 ) = ( 3 , 5 ) (1+2, 2+3) = (3,5) ( 1 + 2 , 2 + 3 ) = ( 3 , 5 ) 5 ≤ 6 5 \le 6 5 ≤ 6 S 1 2 = { ( 2 , 3 ) , ( 3 , 5 ) } S^2_1 = \{(2,3), (3,5)\} S 1 2 = {( 2 , 3 ) , ( 3 , 5 )}
S 2 = merge ( S 1 , S 1 2 ) = merge ( { ( 0 , 0 ) , ( 1 , 2 ) } , { ( 2 , 3 ) , ( 3 , 5 ) } ) S^2 = \text{merge}(S^1, S^2_1) = \text{merge}(\{(0,0), (1,2)\}, \{(2,3), (3,5)\}) S 2 = merge ( S 1 , S 1 2 ) = merge ({( 0 , 0 ) , ( 1 , 2 )} , {( 2 , 3 ) , ( 3 , 5 )}) 比较 ( 0 , 0 ) (0,0) ( 0 , 0 ) S 1 2 S^2_1 S 1 2 比较 ( 1 , 2 ) (1,2) ( 1 , 2 ) S 1 2 S^2_1 S 1 2 ( 1 , 2 ) (1,2) ( 1 , 2 ) ( 2 , 3 ) (2,3) ( 2 , 3 ) W ( 1 , 2 ) = 2 ≱ W ( 2 , 3 ) = 3 W_{(1,2)}=2 \not\ge W_{(2,3)}=3 W ( 1 , 2 ) = 2 ≥ W ( 2 , 3 ) = 3 ( 1 , 2 ) (1,2) ( 1 , 2 ) ( 3 , 5 ) (3,5) ( 3 , 5 ) W ( 1 , 2 ) = 2 ≱ W ( 3 , 5 ) = 5 W_{(1,2)}=2 \not\ge W_{(3,5)}=5 W ( 1 , 2 ) = 2 ≥ W ( 3 , 5 ) = 5 比较 S 1 2 S^2_1 S 1 2 S 1 S^1 S 1 ( 2 , 3 ) (2,3) ( 2 , 3 ) ( 0 , 0 ) (0,0) ( 0 , 0 ) W ( 2 , 3 ) = 3 ≥ W ( 0 , 0 ) = 0 W_{(2,3)}=3 \ge W_{(0,0)}=0 W ( 2 , 3 ) = 3 ≥ W ( 0 , 0 ) = 0 P ( 2 , 3 ) = 2 ≥ P ( 0 , 0 ) = 0 P_{(2,3)}=2 \ge P_{(0,0)}=0 P ( 2 , 3 ) = 2 ≥ P ( 0 , 0 ) = 0 W j ≥ W k W_j \ge W_k W j ≥ W k P j ≤ P k P_j \le P_k P j ≤ P k j j j ( 2 , 3 ) (2,3) ( 2 , 3 ) ( 1 , 2 ) (1,2) ( 1 , 2 ) W ( 2 , 3 ) = 3 ≥ W ( 1 , 2 ) = 2 W_{(2,3)}=3 \ge W_{(1,2)}=2 W ( 2 , 3 ) = 3 ≥ W ( 1 , 2 ) = 2 P ( 2 , 3 ) = 2 ≥ P ( 1 , 2 ) = 1 P_{(2,3)}=2 \ge P_{(1,2)}=1 P ( 2 , 3 ) = 2 ≥ P ( 1 , 2 ) = 1 内部无支配。 S 2 = { ( 0 , 0 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 5 ) } S^2 = \{(0,0), (1,2), (2,3), (3,5)\} S 2 = {( 0 , 0 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 5 )}
i = 3 i=3 i = 3 ( p 3 , w 3 ) = ( 5 , 4 ) (p_3,w_3)=(5,4) ( p 3 , w 3 ) = ( 5 , 4 )
S 2 = { ( 0 , 0 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 5 ) } S^2 = \{(0,0), (1,2), (2,3), (3,5)\} S 2 = {( 0 , 0 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 5 )}
S 1 3 S^3_1 S 1 3 从 ( 0 , 0 ) ∈ S 2 (0,0) \in S^2 ( 0 , 0 ) ∈ S 2 ( 0 + 5 , 0 + 4 ) = ( 5 , 4 ) (0+5, 0+4) = (5,4) ( 0 + 5 , 0 + 4 ) = ( 5 , 4 ) 4 ≤ 6 4 \le 6 4 ≤ 6 从 ( 1 , 2 ) ∈ S 2 (1,2) \in S^2 ( 1 , 2 ) ∈ S 2 ( 1 + 5 , 2 + 4 ) = ( 6 , 6 ) (1+5, 2+4) = (6,6) ( 1 + 5 , 2 + 4 ) = ( 6 , 6 ) 6 ≤ 6 6 \le 6 6 ≤ 6 从 ( 2 , 3 ) ∈ S 2 (2,3) \in S^2 ( 2 , 3 ) ∈ S 2 ( 2 + 5 , 3 + 4 ) = ( 7 , 7 ) (2+5, 3+4) = (7,7) ( 2 + 5 , 3 + 4 ) = ( 7 , 7 ) 76 7 6 76 从 ( 3 , 5 ) ∈ S 2 (3,5) \in S^2 ( 3 , 5 ) ∈ S 2 ( 3 + 5 , 5 + 4 ) = ( 8 , 9 ) (3+5, 5+4) = (8,9) ( 3 + 5 , 5 + 4 ) = ( 8 , 9 ) 96 9 6 96 S 1 3 = { ( 5 , 4 ) , ( 6 , 6 ) } S^3_1 = \{(5,4), (6,6)\} S 1 3 = {( 5 , 4 ) , ( 6 , 6 )}
S 3 = merge ( S 2 , S 1 3 ) = merge ( { ( 0 , 0 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 5 ) } , { ( 5 , 4 ) , ( 6 , 6 ) } ) S^3 = \text{merge}(S^2, S^3_1) = \text{merge}(\{(0,0), (1,2), (2,3), (3,5)\}, \{(5,4), (6,6)\}) S 3 = merge ( S 2 , S 1 3 ) = merge ({( 0 , 0 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 5 )} , {( 5 , 4 ) , ( 6 , 6 )}) 应用支配规则:( P j , W j ) = ( 3 , 5 ) ∈ S 2 (P_j,W_j) = (3,5) \in S^2 ( P j , W j ) = ( 3 , 5 ) ∈ S 2 ( P k , W k ) = ( 5 , 4 ) ∈ S 1 3 (P_k,W_k) = (5,4) \in S^3_1 ( P k , W k ) = ( 5 , 4 ) ∈ S 1 3 这里 W j = 5 ≥ W k = 4 W_j=5 \ge W_k=4 W j = 5 ≥ W k = 4 P j = 3 ≤ P k = 5 P_j=3 \le P_k=5 P j = 3 ≤ P k = 5 ( 5 , 4 ) (5,4) ( 5 , 4 ) ( 3 , 5 ) (3,5) ( 3 , 5 ) ( 3 , 5 ) (3,5) ( 3 , 5 ) S 3 = { ( 0 , 0 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 5 , 4 ) , ( 6 , 6 ) } S^3 = \{(0,0), (1,2), (2,3), (5,4), (6,6)\} S 3 = {( 0 , 0 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 5 , 4 ) , ( 6 , 6 )} S 3 S^3 S 3 P P P ( 6 , 6 ) (6,6) ( 6 , 6 ) 6 6 6
空间复杂度
最坏情况下,如果没有序偶被支配规则清除, ∣ S i ∣ ≈ 2 ∣ S i − 1 ∣ |S^i| \approx 2|S^{i-1}| ∣ S i ∣ ≈ 2∣ S i − 1 ∣ ∣ S 0 ∣ = 1 |S^0|=1 ∣ S 0 ∣ = 1 ∣ S n ∣ ≈ 2 n |S^n| \approx 2^n ∣ S n ∣ ≈ 2 n O ( ∑ ∣ S i ∣ ) = O ( 2 n ) O(\sum |S^i|) = O(2^n) O ( ∑ ∣ S i ∣ ) = O ( 2 n )
时间复杂度
由 S i − 1 S^{i-1} S i − 1 S i S^i S i S 1 i S^i_1 S 1 i ∣ S i − 1 ∣ |S^{i-1}| ∣ S i − 1 ∣ O ( ∑ ∣ S i − 1 ∣ ) = O ( 2 n ) O(\sum |S^{i-1}|) = O(2^n) O ( ∑ ∣ S i − 1 ∣ ) = O ( 2 n )
如果序偶 ( P i , W i ) = ( 2 i , 2 i ) (P_i, W_i)=(2^i, 2^i) ( P i , W i ) = ( 2 i , 2 i )
如果效益 P P P W W W ∣ S i ∣ |S^i| ∣ S i ∣ 1 + ∑ j = 1 i P j 1 + \sum_{j=1}^{i} P_j 1 + ∑ j = 1 i P j 1 + min { ∑ j = 1 i W j , M } 1 + \min\{\sum_{j=1}^{i} W_j, M\} 1 + min { ∑ j = 1 i W j , M }
因此,时间复杂度可以更精确地表示为:
O ( min { 2 n , n ∑ P j , n M } ) O(\min\{2^n, n \sum P_j, nM\}) O ( min { 2 n , n ∑ P j , n M })
当 M M M n M nM n M 伪多项式时间算法 。
序偶对法的改进 (试探法/Probing Method)
为了进一步提高效率,特别是当 n n n 最优解的估计下界 L L L 来提前剪枝。
L L L f n ( M ) ≥ L f_n(M) \ge L f n ( M ) ≥ L L L L L L L
用 PLEFT ( i ) \text{PLEFT}(i) PLEFT ( i ) i + 1 , … , n i+1, \dots, n i + 1 , … , n PLEFT ( i ) = ∑ j = i + 1 n p j \text{PLEFT}(i) = \sum_{j=i+1}^{n} p_j PLEFT ( i ) = ∑ j = i + 1 n p j
剪枝规则 : 在生成 S k S^k S k ( p , w ) ∈ S k (p,w) \in S^k ( p , w ) ∈ S k S k S^k S k p + PLEFT ( k ) < L p + \text{PLEFT}(k) < L p + PLEFT ( k ) < L ( p , w ) (p,w) ( p , w ) p + PLEFT ( k ) p + \text{PLEFT}(k) p + PLEFT ( k ) L L L L L L
改进后算法流程中剪枝的应用:
在形成 S i S^i S i S i − 1 S^{i-1} S i − 1 S 1 i S^i_1 S 1 i S i S^i S i ( p , w ) (p,w) ( p , w ) p + PLEFT ( i ) < L p + \text{PLEFT}(i) < L p + PLEFT ( i ) < L S i S^i S i ( p , w ) (p,w) ( p , w ) S i S^i S i S pruned i S^i_{\text{pruned}} S pruned i S 1 i + 1 S^{i+1}_1 S 1 i + 1 S i + 1 S^{i+1} S i + 1
多段图问题 多段图是一个有向图 ,具有以下特点:
顶点集合被划分为 k ≥ 2 k \geq 2 k ≥ 2 不相交的层次 :
V = V 1 ∪ V 2 ∪ ⋯ ∪ V k V = V_1 \cup V_2 \cup \dots \cup V_k V = V 1 ∪ V 2 ∪ ⋯ ∪ V k
其中:
V 1 = { s } V_1 = \{s\} V 1 = { s } V k = { t } V_k = \{t\} V k = { t } 边的方向只允许从第 i i i i + 1 i+1 i + 1
每条边 ⟨ u , v ⟩ \langle u, v \rangle ⟨ u , v ⟩ 非负权值 c ( u , v ) c(u, v) c ( u , v ) u u u v v v
目标:得到从源点 s s s t t t 。
graph TD
s --> A1[1]
s --> A2[2]
A1 --> B1[3]
A1 --> B2[4]
A2 --> B2
A2 --> B3[5]
B1 --> t
B2 --> t
B3 --> t
问题的最优性原理 :
设已经找到了从 s s s t t t 最短路径 : s → v 2 → v 3 → ⋯ → v k − 1 → t s \rightarrow v_2 \rightarrow v_3 \rightarrow \dots \rightarrow v_{k-1} \rightarrow t s → v 2 → v 3 → ⋯ → v k − 1 → t
s → v 2 → q 3 → ⋯ → t s \rightarrow v_2 \rightarrow q_3 \rightarrow \dots \rightarrow t s → v 2 → q 3 → ⋯ → t
也会更短,与假设矛盾 。
所以多段图问题满足最优性原理 ,可以用动态规划解决。
向前处理法 (从终点往回推)
定义 COST ( i , j ) \text{COST}(i, j) COST ( i , j ) i i i j j j t t t
递推关系:
COST ( i , j ) = min l ∈ V i + 1 { c ( j , l ) + COST ( i + 1 , l ) } \text{COST}(i, j) = \min_{l \in V_{i+1}} \{ c(j, l) + \text{COST}(i+1, l) \} COST ( i , j ) = l ∈ V i + 1 min { c ( j , l ) + COST ( i + 1 , l )}
边界条件:
COST ( k − 1 , j ) = { c ( j , t ) 若 ⟨ j , t ⟩ ∈ E ∞ 否则 \text{COST}(k-1, j) = \begin{cases} c(j, t) & \text{若 } \langle j, t \rangle \in E \\ \infty & \text{否则} \end{cases} COST ( k − 1 , j ) = { c ( j , t ) ∞ 若 ⟨ j , t ⟩ ∈ E 否则
向后处理法 (从起点往后推)
定义 BCOST ( i , j ) \text{BCOST}(i, j) BCOST ( i , j ) s s s i i i j j j 递推关系: BCOST ( i , j ) = min l ∈ V i − 1 { BCOST ( i − 1 , l ) + c ( l , j ) } \text{BCOST}(i, j) = \min_{l \in V_{i-1}} \{ \text{BCOST}(i-1, l) + c(l, j) \} BCOST ( i , j ) = l ∈ V i − 1 min { BCOST ( i − 1 , l ) + c ( l , j )}
BCOST ( s , j ) = { c ( s , j ) 若 ⟨ s , j ⟩ ∈ E ∞ 否则 \text{BCOST}(s, j) = \begin{cases} c(s, j) & \text{若 } \langle s, j \rangle \in E \\ \infty & \text{否则} \end{cases} BCOST ( s , j ) = { c ( s , j ) ∞ 若 ⟨ s , j ⟩ ∈ E 否则
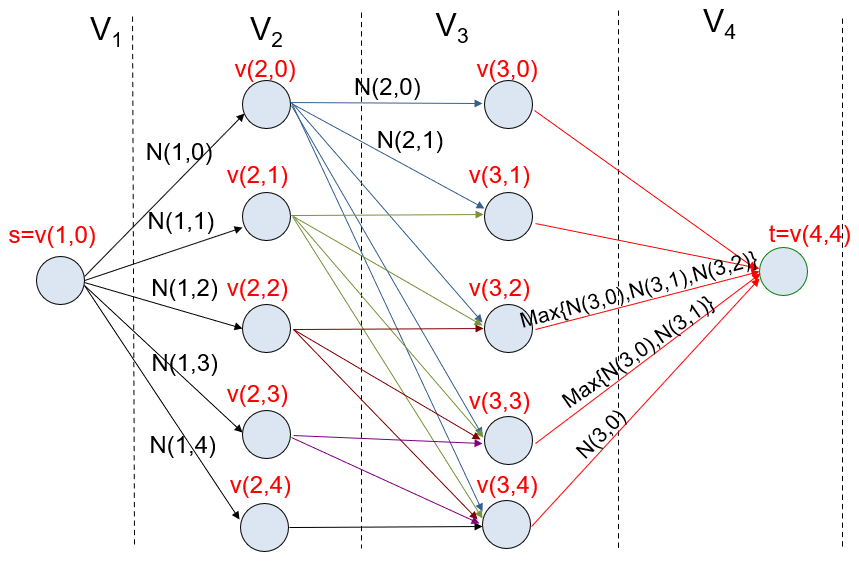
多段图的应用:资源分配问题 假设有 n n n r r r
定义:
N ( i , j ) N(i, j) N ( i , j ) i i i j j j 图中的一个状态 V ( i , j ) V(i, j) V ( i , j ) i − 1 i-1 i − 1 j j j 边:从 V ( i , j ) V(i, j) V ( i , j ) V ( i + 1 , l ) V(i+1, l) V ( i + 1 , l ) i i i l − j l - j l − j 最终问题转化为:从起点 V ( 1 , 0 ) V(1,0) V ( 1 , 0 ) V ( r + 1 , n ) V(r+1, n) V ( r + 1 , n )
旅行商问题 问题的最优性原理 :若一条路径是最短的整条 TSP 路径,那么其任意子路径也必须是最短路径。
设最优路径为:1 → ⋯ → i → … 1 1 \to \dots \to i \to \dots 1 1 → ⋯ → i → … 1 如果从 i i i 1 1 1 这与最优假设矛盾 所以,TSP 满足最优子结构,可以用 动态规划 求解。
状态表示 :
状态转移方程 :
g ( i , S ) = min j ∈ S { c i j + g ( j , S − { j } ) } g(i, S) = \min_{j \in S} \{ c_{ij} + g(j, S - \{j\}) \} g ( i , S ) = j ∈ S min { c ij + g ( j , S − { j })}
最终答案:
g ( 1 , V − { 1 } ) = min k ∈ V − { 1 } { c 1 k + g ( k , V − { 1 , k } ) } g(1, V - \{1\}) = \min_{k \in V-\{1\}} \{ c_{1k} + g(k, V - \{1,k\}) \} g ( 1 , V − { 1 }) = k ∈ V − { 1 } min { c 1 k + g ( k , V − { 1 , k })}
时间复杂度分析 :
对于每一个子集 S S S 2 n − 1 2^{n-1} 2 n − 1 i i i n n n g ( i , S ) g(i, S) g ( i , S ) 每个状态转移要枚举 S S S O ( n ) O(n) O ( n ) 总复杂度是:
O ( n 2 ⋅ 2 n ) O(n^2 \cdot 2^n) O ( n 2 ⋅ 2 n )
比暴力法的 O ( n ! ) O(n!) O ( n !)
例题:状压 dp 吃奶酪
题解可以看这一篇博客 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 #include <bits/stdc++.h> #define endl '\n' using namespace std;typedef long long ll;const int N=20 ;double x[N],y[N];double dis[N][N]={0 };double f[N][40000 ];int n;double ans;inline double cal (int u,int v) return sqrt ((x[u]-x[v])*(x[u]-x[v])+(y[u]-y[v])*(y[u]-y[v]));int main () scanf ("%d" ,&n);memset (f,127 ,sizeof (f));0 ][0 ];for (int i=1 ;i<=n;i++)scanf ("%lf%lf" ,x+i,y+i);for (int i=0 ;i<=n;i++)for (int j=i+1 ;j<=n;j++)cal (i,j);for (int i=1 ;i<=n;i++)1 <<(i-1 )]=dis[i][0 ];for (int i=1 ;i<=n;i++)for (int k=1 ;k<(1 <<n);k++)if ((k&(1 <<(i-1 )))==0 )continue ;for (int j=1 ;j<=n;j++)if (i==j)continue ;if ((k&(1 <<(j-1 )))==0 )continue ;min (f[i][k],f[j][k-(1 <<(i-1 ))]+dis[i][j]);for (int i=1 ;i<=n;i++) min (ans,f[i][(1 <<n)-1 ]);printf ("%.2lf" ,ans);
可靠性设计 该问题旨在设计一个由 n n n
D 1 → D 2 → ⋯ → D n D_1 \rightarrow D_2 \rightarrow \dots \rightarrow D_n D 1 → D 2 → ⋯ → D n
每个设备 D i D_i D i r i r_i r i 串联系统的总可靠性是所有设备可靠性的乘积 ∏ r i \prod r_i ∏ r i 为了提高系统可靠性,可以为每个设备 D i D_i D i D i D_i D i m i m_i m i m i m_i m i D i D_i D i ( 1 − r i ) m i (1-r_i)^{m_i} ( 1 − r i ) m i m i m_i m i D i D_i D i ϕ i ( m i ) = 1 − ( 1 − r i ) m i \phi_i(m_i) = 1 - (1-r_i)^{m_i} ϕ i ( m i ) = 1 − ( 1 − r i ) m i 最优化问题 :在给定的最大总成本 C total C_\text{total} C total D i D_i D i m i m_i m i ∏ i = 1 n ϕ i ( m i ) \prod_{i=1}^n \phi_i(m_i) ∏ i = 1 n ϕ i ( m i )
每种设备至少需要一台。设一台设备 D j D_j D j c j c_j c j D j D_j D j u j u_j u j
u j = ⌊ ( C total + c j − ∑ k = 1 n c k ) / c j ⌋ u_j = \lfloor (C_\text{total} + c_j - \sum_{k=1}^{n} c_k) / c_j \rfloor u j = ⌊( C total + c j − k = 1 ∑ n c k ) / c j ⌋
这个公式确保了在配置 u j u_j u j D j D_j D j D k ( k ≠ j ) D_k (k \neq j) D k ( k = j ) u j u_j u j u j = ⌊ ( C t o t a l − ∑ k ≠ j c k ) / c j ⌋ u_j = \lfloor (C_{total} - \sum_{k \neq j} c_k) / c_j \rfloor u j = ⌊( C t o t a l − ∑ k = j c k ) / c j ⌋ D j D_j D j
此问题可以使用动态规划解决,其思想类似于0/1背包问题中的序偶对法。
定义状态序偶为 (当前累积可靠性, 当前累积成本) ,即 ( f , x ) (f, x) ( f , x )
支配规则 :对于两个序偶 ( f 1 , x 1 ) (f_1, x_1) ( f 1 , x 1 ) ( f 2 , x 2 ) (f_2, x_2) ( f 2 , x 2 ) f 1 ≥ f 2 f_1 \ge f_2 f 1 ≥ f 2 x 1 ≤ x 2 x_1 \le x_2 x 1 ≤ x 2 ( f 1 , x 1 ) (f_1, x_1) ( f 1 , x 1 ) 支配 ( f 2 , x 2 ) (f_2, x_2) ( f 2 , x 2 ) ( f 1 , x 1 ) (f_1, x_1) ( f 1 , x 1 ) ( f 2 , x 2 ) (f_2, x_2) ( f 2 , x 2 )
初始化 :S 0 = { ( 1 , 0 ) } S^0 = \{(1,0)\} S 0 = {( 1 , 0 )} 0 0 0
迭代构造 :S i − 1 S^{i-1} S i − 1 i − 1 i-1 i − 1 S i S^i S i i i i i i i j j j 1 ≤ j ≤ u i 1 \le j \le u_i 1 ≤ j ≤ u i
对 S i − 1 S^{i-1} S i − 1 ( f ′ , x ′ ) ∈ S i − 1 (f', x') \in S^{i-1} ( f ′ , x ′ ) ∈ S i − 1
计算配置 j j j D i D_i D i f new = ϕ i ( j ) × f ′ f_\text{new} = \phi_i(j) \times f' f new = ϕ i ( j ) × f ′ x new = x ′ + c i × j x_\text{new} = x' + c_i \times j x new = x ′ + c i × j
可行性检查 :这个新状态 ( f new , x new ) (f_\text{new}, x_\text{new}) ( f new , x new ) x n e w x_{new} x n e w D i + 1 , … , D n D_{i+1}, \dots, D_n D i + 1 , … , D n C total C_\text{total} C total x n e w + ∑ k = i + 1 n c k ≤ C total x_{new} + \sum_{k=i+1}^{n} c_k \le C_\text{total} x n e w + ∑ k = i + 1 n c k ≤ C total x new x_\text{new} x new C total C_\text{total} C total
所有这样生成的、满足可行性条件的新序偶形成了候选集合。
将所有 j j j 1 1 1 u i u_i u i 支配规则 去除被支配的序偶,最终得到 S i S^i S i
设计一个三级系统 D 1 , D 2 , D 3 D_1, D_2, D_3 D 1 , D 2 , D 3 c 1 = 30 , c 2 = 15 , c 3 = 20 c_1=30, c_2=15, c_3=20 c 1 = 30 , c 2 = 15 , c 3 = 20 r 1 = 0.9 , r 2 = 0.8 , r 3 = 0.5 r_1=0.9, r_2=0.8, r_3=0.5 r 1 = 0.9 , r 2 = 0.8 , r 3 = 0.5 C t o t a l ≤ 105 C_{total} \le 105 C t o t a l ≤ 105
首先计算 u j u_j u j u 1 = ⌊ ( 105 − c 2 − c 3 ) / c 1 ⌋ = ⌊ ( 105 − 15 − 20 ) / 30 ⌋ = ⌊ 70 / 30 ⌋ = 2 u_1 = \lfloor (105 - c_2 - c_3) / c_1 \rfloor = \lfloor (105 - 15 - 20) / 30 \rfloor = \lfloor 70/30 \rfloor = 2 u 1 = ⌊( 105 − c 2 − c 3 ) / c 1 ⌋ = ⌊( 105 − 15 − 20 ) /30 ⌋ = ⌊ 70/30 ⌋ = 2 u 2 = ⌊ ( 105 − c 1 − c 3 ) / c 2 ⌋ = ⌊ ( 105 − 30 − 20 ) / 15 ⌋ = ⌊ 55 / 15 ⌋ = 3 u_2 = \lfloor (105 - c_1 - c_3) / c_2 \rfloor = \lfloor (105 - 30 - 20) / 15 \rfloor = \lfloor 55/15 \rfloor = 3 u 2 = ⌊( 105 − c 1 − c 3 ) / c 2 ⌋ = ⌊( 105 − 30 − 20 ) /15 ⌋ = ⌊ 55/15 ⌋ = 3 u 3 = ⌊ ( 105 − c 1 − c 2 ) / c 3 ⌋ = ⌊ ( 105 − 30 − 15 ) / 20 ⌋ = ⌊ 60 / 20 ⌋ = 3 u_3 = \lfloor (105 - c_1 - c_2) / c_3 \rfloor = \lfloor (105 - 30 - 15) / 20 \rfloor = \lfloor 60/20 \rfloor = 3 u 3 = ⌊( 105 − c 1 − c 2 ) / c 3 ⌋ = ⌊( 105 − 30 − 15 ) /20 ⌋ = ⌊ 60/20 ⌋ = 3
计算各设备不同台数时的可靠性 ϕ i ( m i ) = 1 − ( 1 − r i ) m i \phi_i(m_i) = 1-(1-r_i)^{m_i} ϕ i ( m i ) = 1 − ( 1 − r i ) m i
D 1 ( r 1 = 0.9 ) D_1 (r_1=0.9) D 1 ( r 1 = 0.9 ) ϕ 1 ( 1 ) = 0.9 \phi_1(1)=0.9 ϕ 1 ( 1 ) = 0.9 ϕ 1 ( 2 ) = 1 − ( 0.1 ) 2 = 0.99 \phi_1(2)=1-(0.1)^2=0.99 ϕ 1 ( 2 ) = 1 − ( 0.1 ) 2 = 0.99 D 2 ( r 2 = 0.8 ) D_2 (r_2=0.8) D 2 ( r 2 = 0.8 ) ϕ 2 ( 1 ) = 0.8 \phi_2(1)=0.8 ϕ 2 ( 1 ) = 0.8 ϕ 2 ( 2 ) = 1 − ( 0.2 ) 2 = 0.96 \phi_2(2)=1-(0.2)^2=0.96 ϕ 2 ( 2 ) = 1 − ( 0.2 ) 2 = 0.96 ϕ 2 ( 3 ) = 1 − ( 0.2 ) 3 = 0.992 \phi_2(3)=1-(0.2)^3=0.992 ϕ 2 ( 3 ) = 1 − ( 0.2 ) 3 = 0.992 D 3 ( r 3 = 0.5 ) D_3 (r_3=0.5) D 3 ( r 3 = 0.5 ) ϕ 3 ( 1 ) = 0.5 \phi_3(1)=0.5 ϕ 3 ( 1 ) = 0.5 ϕ 3 ( 2 ) = 1 − ( 0.5 ) 2 = 0.75 \phi_3(2)=1-(0.5)^2=0.75 ϕ 3 ( 2 ) = 1 − ( 0.5 ) 2 = 0.75 ϕ 3 ( 3 ) = 1 − ( 0.5 ) 3 = 0.875 \phi_3(3)=1-(0.5)^3=0.875 ϕ 3 ( 3 ) = 1 − ( 0.5 ) 3 = 0.875 迭代过程: S 0 = { ( 1 , 0 ) } S^0 = \{(1,0)\} S 0 = {( 1 , 0 )}
阶段 i = 1 ( D 1 ) i=1 (D_1) i = 1 ( D 1 ) (最小未来成本 c 2 + c 3 = 15 + 20 = 35 c_2+c_3 = 15+20=35 c 2 + c 3 = 15 + 20 = 35
m 1 = 1 m_1=1 m 1 = 1 ( ϕ 1 ( 1 ) × 1 , 0 + 30 × 1 ) = ( 0.9 , 30 ) (\phi_1(1) \times 1, 0 + 30 \times 1) = (0.9, 30) ( ϕ 1 ( 1 ) × 1 , 0 + 30 × 1 ) = ( 0.9 , 30 ) 30 + 35 = 65 ≤ 105 30+35=65 \le 105 30 + 35 = 65 ≤ 105 m 1 = 2 m_1=2 m 1 = 2 ( ϕ 1 ( 2 ) × 1 , 0 + 30 × 2 ) = ( 0.99 , 60 ) (\phi_1(2) \times 1, 0 + 30 \times 2) = (0.99, 60) ( ϕ 1 ( 2 ) × 1 , 0 + 30 × 2 ) = ( 0.99 , 60 ) 60 + 35 = 95 ≤ 105 60+35=95 \le 105 60 + 35 = 95 ≤ 105 S candidate 1 = { ( 0.9 , 30 ) , ( 0.99 , 60 ) } S^1_{\text{candidate}} = \{(0.9,30), (0.99,60)\} S candidate 1 = {( 0.9 , 30 ) , ( 0.99 , 60 )} S 1 = { ( 0.9 , 30 ) , ( 0.99 , 60 ) } S^1 = \{(0.9,30), (0.99,60)\} S 1 = {( 0.9 , 30 ) , ( 0.99 , 60 )} 阶段 i = 2 ( D 2 ) i=2 (D_2) i = 2 ( D 2 ) (最小未来成本 c 3 = 20 c_3 = 20 c 3 = 20
临时集合 S temp 2 S^2_{\text{temp}} S temp 2
m 2 = 1 ( ϕ 2 ( 1 ) = 0.8 , cost = 15 ) m_2=1 (\phi_2(1)=0.8, \text{cost}=15) m 2 = 1 ( ϕ 2 ( 1 ) = 0.8 , cost = 15 ) 从 ( 0.9 , 30 ) ∈ S 1 (0.9,30) \in S^1 ( 0.9 , 30 ) ∈ S 1 ( 0.8 × 0.9 , 30 + 15 ) = ( 0.72 , 45 ) (0.8 \times 0.9, 30+15) = (0.72, 45) ( 0.8 × 0.9 , 30 + 15 ) = ( 0.72 , 45 ) 45 + 20 = 65 ≤ 105 45+20=65 \le 105 45 + 20 = 65 ≤ 105 从 ( 0.99 , 60 ) ∈ S 1 (0.99,60) \in S^1 ( 0.99 , 60 ) ∈ S 1 ( 0.8 × 0.99 , 60 + 15 ) = ( 0.792 , 75 ) (0.8 \times 0.99, 60+15) = (0.792, 75) ( 0.8 × 0.99 , 60 + 15 ) = ( 0.792 , 75 ) 75 + 20 = 95 ≤ 105 75+20=95 \le 105 75 + 20 = 95 ≤ 105 m 2 = 2 ( ϕ 2 ( 2 ) = 0.96 , cost = 30 ) m_2=2 (\phi_2(2)=0.96, \text{cost}=30) m 2 = 2 ( ϕ 2 ( 2 ) = 0.96 , cost = 30 ) 从 ( 0.9 , 30 ) ∈ S 1 (0.9,30) \in S^1 ( 0.9 , 30 ) ∈ S 1 ( 0.96 × 0.9 , 30 + 30 ) = ( 0.864 , 60 ) (0.96 \times 0.9, 30+30) = (0.864, 60) ( 0.96 × 0.9 , 30 + 30 ) = ( 0.864 , 60 ) 60 + 20 = 80 ≤ 105 60+20=80 \le 105 60 + 20 = 80 ≤ 105 从 ( 0.99 , 60 ) ∈ S 1 (0.99,60) \in S^1 ( 0.99 , 60 ) ∈ S 1 ( 0.96 × 0.99 , 60 + 30 ) = ( 0.9504 , 90 ) (0.96 \times 0.99, 60+30) = (0.9504, 90) ( 0.96 × 0.99 , 60 + 30 ) = ( 0.9504 , 90 ) 90 + 20 = 110 > 105 90+20=110 > 105 90 + 20 = 110 > 105 m 2 = 3 ( ϕ 2 ( 3 ) = 0.992 , cost = 45 ) m_2=3 (\phi_2(3)=0.992, \text{cost}=45) m 2 = 3 ( ϕ 2 ( 3 ) = 0.992 , cost = 45 ) 从 ( 0.9 , 30 ) ∈ S 1 (0.9,30) \in S^1 ( 0.9 , 30 ) ∈ S 1 ( 0.992 × 0.9 , 30 + 45 ) = ( 0.8928 , 75 ) (0.992 \times 0.9, 30+45) = (0.8928, 75) ( 0.992 × 0.9 , 30 + 45 ) = ( 0.8928 , 75 ) 75 + 20 = 95 ≤ 105 75+20=95 \le 105 75 + 20 = 95 ≤ 105 从 ( 0.99 , 60 ) ∈ S 1 (0.99,60) \in S^1 ( 0.99 , 60 ) ∈ S 1 ( 0.992 × 0.99 , 60 + 45 ) = ( 0.98208 , 105 ) (0.992 \times 0.99, 60+45) = (0.98208, 105) ( 0.992 × 0.99 , 60 + 45 ) = ( 0.98208 , 105 ) 105 + 20 = 125 > 105 105+20=125 > 105 105 + 20 = 125 > 105 S candidate 2 = { ( 0.72 , 45 ) , ( 0.792 , 75 ) , ( 0.864 , 60 ) , ( 0.8928 , 75 ) } S^2_{\text{candidate}} = \{(0.72,45), (0.792,75), (0.864,60), (0.8928,75)\} S candidate 2 = {( 0.72 , 45 ) , ( 0.792 , 75 ) , ( 0.864 , 60 ) , ( 0.8928 , 75 )} 应用支配规则:( 0.8928 , 75 ) (0.8928,75) ( 0.8928 , 75 ) ( 0.792 , 75 ) (0.792,75) ( 0.792 , 75 ) 0.8928 > 0.792 0.8928 > 0.792 0.8928 > 0.792 75 = 75 75=75 75 = 75 S 2 = { ( 0.72 , 45 ) , ( 0.864 , 60 ) , ( 0.8928 , 75 ) } S^2 = \{(0.72,45), (0.864,60), (0.8928,75)\} S 2 = {( 0.72 , 45 ) , ( 0.864 , 60 ) , ( 0.8928 , 75 )} 阶段 i = 3 ( D 3 ) i=3 (D_3) i = 3 ( D 3 ) (最小未来成本 0 0 0
临时集合 S temp 3 S^3_{\text{temp}} S temp 3
m 3 = 1 ( ϕ 3 ( 1 ) = 0.5 , cost = 20 ) m_3=1 (\phi_3(1)=0.5, \text{cost}=20) m 3 = 1 ( ϕ 3 ( 1 ) = 0.5 , cost = 20 ) 从 ( 0.72 , 45 ) ∈ S 2 (0.72,45) \in S^2 ( 0.72 , 45 ) ∈ S 2 ( 0.5 × 0.72 , 45 + 20 ) = ( 0.36 , 65 ) (0.5 \times 0.72, 45+20) = (0.36, 65) ( 0.5 × 0.72 , 45 + 20 ) = ( 0.36 , 65 ) 65 ≤ 105 65 \le 105 65 ≤ 105 从 ( 0.864 , 60 ) ∈ S 2 (0.864,60) \in S^2 ( 0.864 , 60 ) ∈ S 2 ( 0.5 × 0.864 , 60 + 20 ) = ( 0.432 , 80 ) (0.5 \times 0.864, 60+20) = (0.432, 80) ( 0.5 × 0.864 , 60 + 20 ) = ( 0.432 , 80 ) 80 ≤ 105 80 \le 105 80 ≤ 105 从 ( 0.8928 , 75 ) ∈ S 2 (0.8928,75) \in S^2 ( 0.8928 , 75 ) ∈ S 2 ( 0.5 × 0.8928 , 75 + 20 ) = ( 0.4464 , 95 ) (0.5 \times 0.8928, 75+20) = (0.4464, 95) ( 0.5 × 0.8928 , 75 + 20 ) = ( 0.4464 , 95 ) 95 ≤ 105 95 \le 105 95 ≤ 105 m 3 = 2 ( ϕ 3 ( 2 ) = 0.75 , cost = 40 ) m_3=2 (\phi_3(2)=0.75, \text{cost}=40) m 3 = 2 ( ϕ 3 ( 2 ) = 0.75 , cost = 40 ) 从 ( 0.72 , 45 ) ∈ S 2 (0.72,45) \in S^2 ( 0.72 , 45 ) ∈ S 2 ( 0.75 × 0.72 , 45 + 40 ) = ( 0.54 , 85 ) (0.75 \times 0.72, 45+40) = (0.54, 85) ( 0.75 × 0.72 , 45 + 40 ) = ( 0.54 , 85 ) 85 ≤ 105 85 \le 105 85 ≤ 105 从 ( 0.864 , 60 ) ∈ S 2 (0.864,60) \in S^2 ( 0.864 , 60 ) ∈ S 2 ( 0.75 × 0.864 , 60 + 40 ) = ( 0.648 , 100 ) (0.75 \times 0.864, 60+40) = (0.648, 100) ( 0.75 × 0.864 , 60 + 40 ) = ( 0.648 , 100 ) 100 ≤ 105 100 \le 105 100 ≤ 105 从 ( 0.8928 , 75 ) ∈ S 2 (0.8928,75) \in S^2 ( 0.8928 , 75 ) ∈ S 2 ( 0.75 × 0.8928 , 75 + 40 ) = ( 0.6696 , 115 ) (0.75 \times 0.8928, 75+40) = (0.6696, 115) ( 0.75 × 0.8928 , 75 + 40 ) = ( 0.6696 , 115 ) 115 > 105 115 > 105 115 > 105 m 3 = 3 ( ϕ 3 ( 3 ) = 0.875 , cost = 60 ) m_3=3 (\phi_3(3)=0.875, \text{cost}=60) m 3 = 3 ( ϕ 3 ( 3 ) = 0.875 , cost = 60 ) 从 ( 0.72 , 45 ) ∈ S 2 (0.72,45) \in S^2 ( 0.72 , 45 ) ∈ S 2 ( 0.875 × 0.72 , 45 + 60 ) = ( 0.63 , 105 ) (0.875 \times 0.72, 45+60) = (0.63, 105) ( 0.875 × 0.72 , 45 + 60 ) = ( 0.63 , 105 ) 105 ≤ 105 105 \le 105 105 ≤ 105 从 ( 0.864 , 60 ) ∈ S 2 (0.864,60) \in S^2 ( 0.864 , 60 ) ∈ S 2 ( 0.875 × 0.864 , 60 + 60 ) = ( 0.756 , 120 ) (0.875 \times 0.864, 60+60) = (0.756, 120) ( 0.875 × 0.864 , 60 + 60 ) = ( 0.756 , 120 ) 120 > 105 120 > 105 120 > 105 从 ( 0.8928 , 75 ) ∈ S 2 (0.8928,75) \in S^2 ( 0.8928 , 75 ) ∈ S 2 ( 0.875 × 0.8928 , 75 + 60 ) = ( 0.7812 , 135 ) (0.875 \times 0.8928, 75+60) = (0.7812, 135) ( 0.875 × 0.8928 , 75 + 60 ) = ( 0.7812 , 135 ) 135 > 105 135 > 105 135 > 105 S candidate 3 = { ( 0.36 , 65 ) , ( 0.432 , 80 ) , ( 0.4464 , 95 ) , ( 0.54 , 85 ) , ( 0.648 , 100 ) , ( 0.63 , 105 ) } S^3_{\text{candidate}} = \{(0.36,65), (0.432,80), (0.4464,95), (0.54,85), (0.648,100), (0.63,105)\} S candidate 3 = {( 0.36 , 65 ) , ( 0.432 , 80 ) , ( 0.4464 , 95 ) , ( 0.54 , 85 ) , ( 0.648 , 100 ) , ( 0.63 , 105 )} 应用支配规则:(在此集合中,没有元素互相支配)。S 3 = { ( 0.36 , 65 ) , ( 0.432 , 80 ) , ( 0.4464 , 95 ) , ( 0.54 , 85 ) , ( 0.648 , 100 ) , ( 0.63 , 105 ) } S^3 = \{(0.36,65), (0.432,80), (0.4464,95), (0.54,85), (0.648,100), (0.63,105)\} S 3 = {( 0.36 , 65 ) , ( 0.432 , 80 ) , ( 0.4464 , 95 ) , ( 0.54 , 85 ) , ( 0.648 , 100 ) , ( 0.63 , 105 )} 最优解与回溯 :S 3 S^3 S 3 ( 0.648 , 100 ) (0.648, 100) ( 0.648 , 100 )
该序偶 ( 0.648 , 100 ) (0.648, 100) ( 0.648 , 100 ) D 3 D_3 D 3 m 3 = 2 m_3=2 m 3 = 2 S 2 3 S^3_2 S 2 3 ϕ 3 ( 2 ) = 0.75 \phi_3(2)=0.75 ϕ 3 ( 2 ) = 0.75 ( f ′ , x ′ ) (f', x') ( f ′ , x ′ ) 0.75 × f ′ = 0.648 ⇒ f ′ = 0.864 0.75 \times f' = 0.648 \Rightarrow f'=0.864 0.75 × f ′ = 0.648 ⇒ f ′ = 0.864 x ′ + 20 × 2 = 100 ⇒ x ′ = 60 x' + 20 \times 2 = 100 \Rightarrow x'=60 x ′ + 20 × 2 = 100 ⇒ x ′ = 60 ( 0.864 , 60 ) ∈ S 2 (0.864, 60) \in S^2 ( 0.864 , 60 ) ∈ S 2 序偶 ( 0.864 , 60 ) (0.864, 60) ( 0.864 , 60 ) D 2 D_2 D 2 m 2 = 2 m_2=2 m 2 = 2 S 2 2 S^2_2 S 2 2 ϕ 2 ( 2 ) = 0.96 \phi_2(2)=0.96 ϕ 2 ( 2 ) = 0.96 ( f ′ ′ , x ′ ′ ) (f'', x'') ( f ′′ , x ′′ ) 0.96 × f ′ ′ = 0.864 ⇒ f ′ ′ = 0.9 0.96 \times f'' = 0.864 \Rightarrow f''=0.9 0.96 × f ′′ = 0.864 ⇒ f ′′ = 0.9 x ′ ′ + 15 × 2 = 60 ⇒ x ′ ′ = 30 x'' + 15 \times 2 = 60 \Rightarrow x''=30 x ′′ + 15 × 2 = 60 ⇒ x ′′ = 30 ( 0.9 , 30 ) ∈ S 1 (0.9, 30) \in S^1 ( 0.9 , 30 ) ∈ S 1 序偶 ( 0.9 , 30 ) (0.9, 30) ( 0.9 , 30 ) D 1 D_1 D 1 m 1 = 1 m_1=1 m 1 = 1 S 1 1 S^1_1 S 1 1 ϕ 1 ( 1 ) = 0.9 \phi_1(1)=0.9 ϕ 1 ( 1 ) = 0.9 ( f ′ ′ ′ , x ′ ′ ′ ) (f''', x''') ( f ′′′ , x ′′′ ) 0.9 × f ′ ′ ′ = 0.9 ⇒ f ′ ′ ′ = 1 0.9 \times f''' = 0.9 \Rightarrow f'''=1 0.9 × f ′′′ = 0.9 ⇒ f ′′′ = 1 x ′ ′ ′ + 30 × 1 = 30 ⇒ x ′ ′ ′ = 0 x''' + 30 \times 1 = 30 \Rightarrow x'''=0 x ′′′ + 30 × 1 = 30 ⇒ x ′′′ = 0 ( 1 , 0 ) ∈ S 0 (1,0) \in S^0 ( 1 , 0 ) ∈ S 0 决策序列为 ( m 1 , m 2 , m 3 ) = ( 1 , 2 , 2 ) (m_1, m_2, m_3) = (1,2,2) ( m 1 , m 2 , m 3 ) = ( 1 , 2 , 2 ) 0.648 0.648 0.648 1 × 30 + 2 × 15 + 2 × 20 = 30 + 30 + 40 = 100 ≤ 105 1 \times 30 + 2 \times 15 + 2 \times 20 = 30+30+40 = 100 \le 105 1 × 30 + 2 × 15 + 2 × 20 = 30 + 30 + 40 = 100 ≤ 105
最优二分检索树 (OBST) 给定一个已排序的标识符(键)集合 A = { a 1 , a 2 , … , a n } A = \{a_1, a_2, \dots, a_n\} A = { a 1 , a 2 , … , a n } a 1 < a 2 < ⋯ < a n a_1 < a_2 < \dots < a_n a 1 < a 2 < ⋯ < a n
P ( i ) P(i) P ( i ) a i a_i a i Q ( i ) Q(i) Q ( i ) X X X a i < X < a i + 1 a_i < X < a_{i+1} a i < X < a i + 1 0 ≤ i ≤ n 0 \le i \le n 0 ≤ i ≤ n a 0 = − ∞ , a n + 1 = + ∞ a_0 = -\infty, a_{n+1} = +\infty a 0 = − ∞ , a n + 1 = + ∞ 所有概率之和为1: ∑ i = 1 n P ( i ) + ∑ i = 0 n Q ( i ) = 1 \sum_{i=1}^n P(i) + \sum_{i=0}^n Q(i) = 1 ∑ i = 1 n P ( i ) + ∑ i = 0 n Q ( i ) = 1 目标 :构造一棵二分检索树 (BST),使其预期检索成本(平均比较次数)最小。
二分检索树的预期成本 对于一棵给定的BST T T T
如果根节点是 a k a_k a k level ( a k ) = 1 \text{level}(a_k)=1 level ( a k ) = 1 成功检索 a i a_i a i P ( i ) × level T ( a i ) P(i) \times \text{level}_T(a_i) P ( i ) × level T ( a i ) 不成功检索(落入区间 E i E_i E i Q ( i ) × ( level T ( E i ) − 1 ) Q(i) \times (\text{level}_T(E_i)-1) Q ( i ) × ( level T ( E i ) − 1 ) 或者,如果定义外部节点的层级,并且比较次数是到外部节点的层级,则为 Q ( i ) × level T ( E i ) Q(i) \times \text{level}_T(E_i) Q ( i ) × level T ( E i ) 公式为: ∑ P ( i ) ⋅ level ( a i ) + ∑ Q ( i ) ⋅ ( level ( E i ) − 1 ) \sum P(i) \cdot \text{level}(a_i) + \sum Q(i) \cdot (\text{level}(E_i)-1) ∑ P ( i ) ⋅ level ( a i ) + ∑ Q ( i ) ⋅ ( level ( E i ) − 1 ) 如果一个子树 T i j T_{ij} T ij a i + 1 , … , a j a_{i+1}, \dots, a_j a i + 1 , … , a j E i , … , E j E_i, \dots, E_j E i , … , E j a k a_k a k T i j T_{ij} T ij T i j T_{ij} T ij a k a_k a k
所以定义 W ( i , j ) = ∑ l = i + 1 j P ( l ) + ∑ l = i j Q ( l ) W(i,j) = \sum_{l=i+1}^{j} P(l) + \sum_{l=i}^{j} Q(l) W ( i , j ) = ∑ l = i + 1 j P ( l ) + ∑ l = i j Q ( l ) T i j T_{ij} T ij a i + 1 … a j a_{i+1}\dots a_j a i + 1 … a j E i … E j E_i\dots E_j E i … E j
令 C ( i , j ) C(i,j) C ( i , j ) a i + 1 , … , a j a_{i+1}, \dots, a_j a i + 1 , … , a j E i , … , E j E_i, \dots, E_j E i , … , E j
如果选择 a k a_k a k i < k ≤ j i < k \le j i < k ≤ j T i j T_{ij} T ij
左子树 T i , k − 1 T_{i,k-1} T i , k − 1 a i + 1 , … , a k − 1 a_{i+1}, \dots, a_{k-1} a i + 1 , … , a k − 1 E i , … , E k − 1 E_i, \dots, E_{k-1} E i , … , E k − 1 C ( i , k − 1 ) C(i,k-1) C ( i , k − 1 ) 右子树 T k , j T_{k,j} T k , j a k + 1 , … , a j a_{k+1}, \dots, a_j a k + 1 , … , a j E k , … , E j E_k, \dots, E_j E k , … , E j C ( k , j ) C(k,j) C ( k , j ) 当 a k a_k a k W ( i , j ) W(i,j) W ( i , j ) P ( k ) P(k) P ( k ) W ( i , j ) W(i,j) W ( i , j ) P ( k ) P(k) P ( k ) P ( l ) P(l) P ( l ) Q ( l ) Q(l) Q ( l ) 递推关系式为:
C ( i , j ) = min i < k ≤ j { C ( i , k − 1 ) + C ( k , j ) + W ( i , j ) } C(i,j) = \min_{i<k \le j} \{ C(i,k-1) + C(k,j) + W(i,j) \} C ( i , j ) = i < k ≤ j min { C ( i , k − 1 ) + C ( k , j ) + W ( i , j )}
其中 W ( i , j ) = W ( i , j − 1 ) + P ( j ) + Q ( j ) W(i,j) = W(i,j-1) + P(j) + Q(j) W ( i , j ) = W ( i , j − 1 ) + P ( j ) + Q ( j )
边界条件 :
C ( i , i ) = 0 C(i,i) = 0 C ( i , i ) = 0 W ( i , i ) = Q ( i ) W(i,i)=Q(i) W ( i , i ) = Q ( i ) W ( i , i ) = Q ( i ) W(i,i) = Q(i) W ( i , i ) = Q ( i ) E i E_i E i R ( i , j ) R(i,j) R ( i , j ) C ( i , j ) C(i,j) C ( i , j ) a k a_k a k k k k
问题求解过程 (自底向上):
初始化 (子树中包含0个或1个内部节点):对于 j = i j=i j = i
W ( i , i ) = Q ( i ) C ( i , i ) = 0 R ( i , i ) = inf or 0 \begin{align*} W(i,i) &= Q(i)\\ C(i,i) &= 0\\ R(i,i) &= \inf \text{ or } 0\\ \end{align*} W ( i , i ) C ( i , i ) R ( i , i ) = Q ( i ) = 0 = inf or 0
对于 j = i + 1 j=i+1 j = i + 1
W ( i , i + 1 ) = ∑ l = i + 1 i + 1 P ( l ) + ∑ l = i i + 1 Q ( l ) = Q ( i ) + P ( i + 1 ) + Q ( i + 1 ) C ( i , i + 1 ) = C ( i , i ) + C ( i + 1 , i + 1 ) + W ( i , i + 1 ) = 0 + 0 + W ( i , i + 1 ) = W ( i , i + 1 ) R ( i , i + 1 ) = i + 1 \begin{align*} W(i,i+1) &= \sum_{l=i+1}^{i+1} P(l) + \sum_{l=i}^{i+1} Q(l) \\ &=\boxed{Q(i) + P(i+1) + Q(i+1)}\\ C(i,i+1) &= C(i,i) + C(i+1,i+1) + W(i,i+1) \\ &= 0 + 0 + W(i,i+1) \\ &= \boxed{W(i,i+1)}\\ R(i,i+1) &= \boxed{i+1} \end{align*} W ( i , i + 1 ) C ( i , i + 1 ) R ( i , i + 1 ) = l = i + 1 ∑ i + 1 P ( l ) + l = i ∑ i + 1 Q ( l ) = Q ( i ) + P ( i + 1 ) + Q ( i + 1 ) = C ( i , i ) + C ( i + 1 , i + 1 ) + W ( i , i + 1 ) = 0 + 0 + W ( i , i + 1 ) = W ( i , i + 1 ) = i + 1
j = i + 1 j=i+1 j = i + 1 a i + 1 a_{i+1} a i + 1
迭代 :对于子树中内部节点数量 j − i = 2 , … , n j-i = 2, \dots, n j − i = 2 , … , n 1 2 3 4 5 令 j = i + m。
最终,C ( 0 , n ) C(0,n) C ( 0 , n ) { a 1 , … , a n } \{a_1, \dots, a_n\} { a 1 , … , a n } E 0 , … , E n E_0, \dots, E_n E 0 , … , E n R ( i , j ) R(i,j) R ( i , j )
时间复杂度分析 :
有 O ( n 2 ) O(n^2) O ( n 2 ) C ( i , j ) C(i,j) C ( i , j ) 对于每个 C ( i , j ) C(i,j) C ( i , j ) m = j − i m = j-i m = j − i k k k 总时间复杂度 O ( n 3 ) O(n^3) O ( n 3 ) 对于标识符集 ( a 1 , a 2 , a 3 , a 4 ) = ( end , goto , print , stop ) (a_1,a_2,a_3,a_4)=(\text{end}, \text{goto}, \text{print}, \text{stop}) ( a 1 , a 2 , a 3 , a 4 ) = ( end , goto , print , stop ) P ( 1 ) = 1 / 20 , P ( 2 ) = 1 / 5 , P ( 3 ) = 1 / 10 , P ( 4 ) = 1 / 20 P(1)=1/20, P(2)=1/5, P(3)=1/10, P(4)=1/20 P ( 1 ) = 1/20 , P ( 2 ) = 1/5 , P ( 3 ) = 1/10 , P ( 4 ) = 1/20 Q ( 0 ) = 1 / 5 , Q ( 1 ) = 1 / 10 , Q ( 2 ) = 1 / 5 , Q ( 3 ) = 1 / 20 , Q ( 4 ) = 1 / 20 Q(0)=1/5, Q(1)=1/10, Q(2)=1/5, Q(3)=1/20, Q(4)=1/20 Q ( 0 ) = 1/5 , Q ( 1 ) = 1/10 , Q ( 2 ) = 1/5 , Q ( 3 ) = 1/20 , Q ( 4 ) = 1/20
用构造最优二分检索树的算法 OBST,对其计算 W ( i , j ) W(i ,j) W ( i , j ) R ( i , j ) R(i, j) R ( i , j ) C ( i , j ) C(i, j) C ( i , j ) ( 0 ≤ i , j ≤ 4 ) (0\le i, j\le 4) ( 0 ≤ i , j ≤ 4 )
按公式迭代计算即可,注意细节。
graph TD
A[goto]-->B[end]
A-->C[print]
C-->D[stop]
Knuth的优化方法 Knuth 发现,使得 C ( i , j ) C(i,j) C ( i , j ) k k k R ( i , j ) R(i,j) R ( i , j )
R ( i , j − 1 ) ≤ R ( i , j ) ≤ R ( i + 1 , j ) R(i,j-1) \le R(i,j) \le R(i+1,j) R ( i , j − 1 ) ≤ R ( i , j ) ≤ R ( i + 1 , j )
这意味着在计算 C ( i , j ) C(i,j) C ( i , j ) k k k j − i j-i j − i R ( i + 1 , j ) − R ( i , j − 1 ) + 1 R(i+1,j) - R(i,j-1) + 1 R ( i + 1 , j ) − R ( i , j − 1 ) + 1 而这个选择范围一般很小很小,无需遍历 ,这一层的维度就降下来了。
利用这个性质,可以将计算所有 C ( i , j ) C(i,j) C ( i , j ) O ( n 2 ) O(n^2) O ( n 2 )
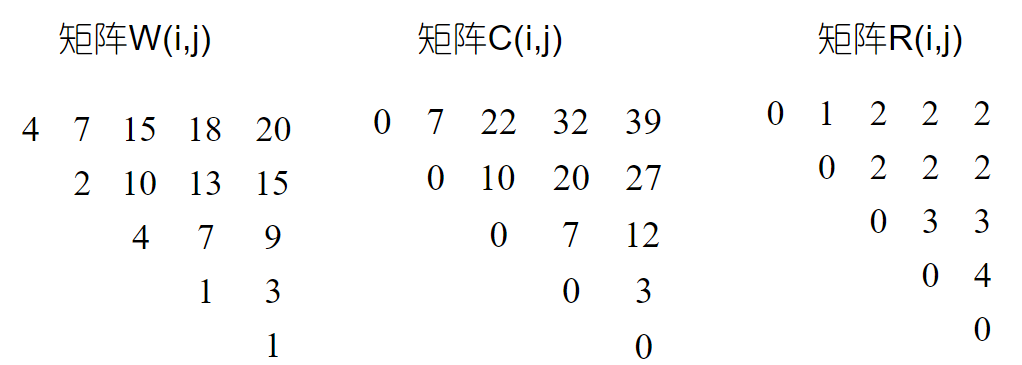
矩阵链乘积问题 给定一个由 n n n A 1 , A 2 , … , A n A_1, A_2, \dots, A_n A 1 , A 2 , … , A n A 1 A 2 … A n A_1 A_2 \dots A_n A 1 A 2 … A n
目标 :找到一种最优的加括号方式,使得计算矩阵链乘积所需的总标量乘法次数最少。
计算代价 :假设矩阵 A A A p × q p \times q p × q B B B q × r q \times r q × r A B AB A B p × r p \times r p × r p × q × r p \times q \times r p × q × r
穷举法 :尝试所有可能的加括号方式。可能的加括号方式数量与 Catalan 数有关,呈指数级增长,对于较大的 n n n 动态规划法 :此问题适合用动态规划解决,因为它具备以下两个核心性质:最优子结构 :一个问题的最优解包含其子问题的最优解。如果计算 A i … A j A_i \dots A_j A i … A j A k A_k A k A k + 1 A_{k+1} A k + 1 ( ( A i … A k ) ( A k + 1 … A j ) ) ((A_i \dots A_k)(A_{k+1} \dots A_j)) (( A i … A k ) ( A k + 1 … A j )) ( A i … A k ) (A_i \dots A_k) ( A i … A k ) ( A k + 1 … A j ) (A_{k+1} \dots A_j) ( A k + 1 … A j ) 重叠子问题 :在求解过程中,许多子问题会被多次重复计算。例如,计算 A 1 A 2 A 3 A 4 A_1 A_2 A_3 A_4 A 1 A 2 A 3 A 4 A 2 A 3 A_2 A_3 A 2 A 3 递推关系式设计 A t A_t A t p t − 1 × p t p_{t-1} \times p_t p t − 1 × p t A i A i + 1 … A j A_i A_{i+1} \dots A_j A i A i + 1 … A j m [ i , j ] m[i, j] m [ i , j ] A i … A j A_i \dots A_j A i … A j
基本情况 :如果 i = j i=j i = j A i A_i A i m [ i , i ] = 0 m[i, i] = 0 m [ i , i ] = 0
递归情况 :如果 i < j i < j i < j k k k i ≤ k < j i \le k < j i ≤ k < j A i … A j A_i \dots A_j A i … A j ( A i … A k ) (A_i \dots A_k) ( A i … A k ) ( A k + 1 … A j ) (A_{k+1} \dots A_j) ( A k + 1 … A j )
计算 ( A i … A k ) (A_i \dots A_k) ( A i … A k ) m [ i , k ] m[i, k] m [ i , k ]
计算 ( A k + 1 … A j ) (A_{k+1} \dots A_j) ( A k + 1 … A j ) m [ k + 1 , j ] m[k+1, j] m [ k + 1 , j ]
将这两个结果矩阵相乘的代价:( A i … A k ) (A_i \dots A_k) ( A i … A k ) p i − 1 × p k p_{i-1} \times p_k p i − 1 × p k ( A k + 1 … A j ) (A_{k+1} \dots A_j) ( A k + 1 … A j ) p k × p j p_k \times p_j p k × p j p i − 1 ⋅ p k ⋅ p j p_{i-1} \cdot p_k \cdot p_j p i − 1 ⋅ p k ⋅ p j
我们需要遍历所有可能的分割点 k k k i ≤ k < j i \le k < j i ≤ k < j k k k m [ i , j ] = min i ≤ k < j { m [ i , k ] + m [ k + 1 , j ] + p i − 1 ⋅ p k ⋅ p j } m[i, j] = \min_{i \le k < j} \{ m[i, k] + m[k+1, j] + p_{i-1} \cdot p_k \cdot p_j \} m [ i , j ] = min i ≤ k < j { m [ i , k ] + m [ k + 1 , j ] + p i − 1 ⋅ p k ⋅ p j }
总结递推式 :
m [ i , j ] = { 0 , if i = j min i ≤ k < j { m [ i , k ] + m [ k + 1 , j ] + p i − 1 p k p j } , if i < j m[i, j] = \begin{cases} 0, & \text{if } i=j \\ \min_{i \le k < j} \{m[i, k] + m[k+1, j] + p_{i-1} p_k p_j\}, & \text{if } i<j \end{cases} m [ i , j ] = { 0 , min i ≤ k < j { m [ i , k ] + m [ k + 1 , j ] + p i − 1 p k p j } , if i = j if i < j
我们还需要一个辅助表 s [ i , j ] s[i,j] s [ i , j ] m [ i , j ] m[i,j] m [ i , j ] k k k
自底向上实现L L L m [ i , j ] m[i,j] m [ i , j ]
L = 1 L=1 L = 1 A i A_i A i m [ i , i ] = 0 m[i,i] = 0 m [ i , i ] = 0 i = 1 , … , n i=1, \dots, n i = 1 , … , n L = 2 L=2 L = 2 A i A i + 1 A_i A_{i+1} A i A i + 1 m [ i , i + 1 ] = m [ i , i ] + m [ i + 1 , i + 1 ] + p i − 1 p i p i + 1 = p i − 1 p i p i + 1 m[i,i+1] = m[i,i] + m[i+1,i+1] + p_{i-1} p_i p_{i+1} = p_{i-1} p_i p_{i+1} m [ i , i + 1 ] = m [ i , i ] + m [ i + 1 , i + 1 ] + p i − 1 p i p i + 1 = p i − 1 p i p i + 1 i = 1 , … , n − 1 i=1, \dots, n-1 i = 1 , … , n − 1 s [ i , i + 1 ] = i s[i,i+1] = i s [ i , i + 1 ] = i L = 3 , … , n L=3, \dots, n L = 3 , … , n L L L i i i 1 1 1 n − L + 1 n-L+1 n − L + 1 j = i + L − 1 j = i+L-1 j = i + L − 1 ( i , j ) (i,j) ( i , j ) k k k i i i j − 1 j-1 j − 1 m [ i , j ] m[i,j] m [ i , j ] s [ i , j ] s[i,j] s [ i , j ] 最终,m [ 1 , n ] m[1,n] m [ 1 , n ] A 1 … A n A_1 \dots A_n A 1 … A n
其他例题 找零钱问题 已知有 m m m d 1 < d 2 < ⋯ < d m d_1<d_2<\dots<d_m d 1 < d 2 < ⋯ < d m d 1 = 1 d_1=1 d 1 = 1 n n n
记 n n n F ( n ) F(n) F ( n )
F ( 0 ) = 0 F(0)=0 F ( 0 ) = 0 0 0 0 F ( 1 ) = 1 F(1)=1 F ( 1 ) = 1 状态转移方程:
F ( n ) = min F ( n − d j ) + 1 F(n)=\min{F(n-d_j)}+1 F ( n ) = min F ( n − d j ) + 1
1 2 3 4 5 6 7 8 9 10 11 coins = [1 , ..., m]def solve (coins, n ):float ('inf' )] * (n + 1 )0 ] = 0 for coin in coins:for i in range (0 , n + 1 ):min (dp[i], dp[i - coin] + 1 )return dp[n]
回文字符串 将字符串表示为 C 1 C 2 … C n C_1C_2\dots C_n C 1 C 2 … C n C i C_i C i C j C_j C j n ( i , j ) n(i,j) n ( i , j )
若 C i = C j C_i=C_j C i = C j C i + 1 … C j − 1 C_{i+1}\dots C_{j-1} C i + 1 … C j − 1 否则,考虑 C ( i + 1 ) … C j C_(i+1)\dots C_j C ( i + 1 ) … C j C ( i ) … C ( j − 1 ) C_(i)\dots C_(j-1) C ( i ) … C ( j − 1 ) 对于前者:需要在 C j C_j C j C i C_i C i 对于后者:需要在 C i C_i C i C j C_j C j 递推关系式:
当 j − i ≥ 1 j-i\ge 1 j − i ≥ 1 若 C i = C j C_i=C_j C i = C j n ( i , j ) = n ( i + 1 , j − 1 ) n(i,j)=n(i+1,j-1) n ( i , j ) = n ( i + 1 , j − 1 ) 若 C i ≠ C j C_i\ne C_j C i = C j n ( i , j ) = min { n ( i + 1 , j ) , n ( i , j − 1 ) } + 1 n(i,j)=\min\{n(i+1,j),n(i,j-1)\}+1 n ( i , j ) = min { n ( i + 1 , j ) , n ( i , j − 1 )} + 1 当 j − i < 1 j-i<1 j − i < 1 LCS 问题 最长公共子序列问题 n n n A A A m m m B B B n , m ≤ 5000 n,m \leq 5000 n , m ≤ 5000 A A A B B B
LNDS 问题 最长不下降子序列问题
回溯法 回溯法是一种系统地搜索问题所有可能解或最优解 的算法策略。
当问题可以被分解为一系列步骤,并且在每一步都有多种选择时,回溯法会尝试每一种选择。如果发现当前选择不能导致一个有效的解(或者不是最优解),它就会“回溯”到上一步,尝试其他的选择。
相关概念如下:
多阶段决策问题 (组合问题):问题的解决过程可以看作是一系列决策的结果。例如,在 N N N
解向量表示 :问题的解可以用一个元组(向量)来表示,例如 ( x 1 , x 2 , … , x n ) (x_1, x_2, \dots, x_n) ( x 1 , x 2 , … , x n )
固定长度元组 :解向量的长度是固定的,例如 N N N N N N N N N 不定长度元组 :解向量的长度是不确定的,例如子集和问题中,找到的子集包含的元素个数是不固定的。约束条件 :问题的解必须满足一定的约束条件。
显式约束 :对解向量中每个分量的取值范围的限制。例如,在 0-1 背包问题中,物品要么选(x i = 1 x_i=1 x i = 1 x i = 0 x_i=0 x i = 0 隐式约束 :对解向量中不同分量之间关系的限制,或者对整个解向量的限制。例如, N N N 描述了 x i x_i x i 与问题实例有关 。 多米诺性质 :这是回溯法能够高效工作的关键特性。
多米诺性质指的是,如果一个部分构造的解向量 ( x 1 , … , x i ) (x_1, \dots, x_i) ( x 1 , … , x i ) ( x 1 , … , x i , x i + 1 , … , x n ) (x_1, \dots, x_i, x_{i+1}, \dots, x_n) ( x 1 , … , x i , x i + 1 , … , x n ) 提前剪枝 :根据多米诺性质,如果发现当前正在构建的部分解 ( x 1 , … , x i ) (x_1, \dots, x_i) ( x 1 , … , x i ) x i + 1 , … , x n x_{i+1}, \dots, x_n x i + 1 , … , x n 限界函数 :在回溯法中,我们通常会定义一个限界函数 B ( x 1 , … , x i ) B(x_1, \dots, x_i) B ( x 1 , … , x i ) B B B 相比于硬性处理 ,即生成所有可能的解向量,然后逐一检查它们是否满足所有约束条件(如果每个 x i x_i x i m i m_i m i m 1 × m 2 × ⋯ × m n m_1 \times m_2 \times \dots \times m_n m 1 × m 2 × ⋯ × m n 可以利用多米诺性质 :通过限界函数在构造过程中提前判断,如果发现部分解 ( x 1 , … , x i ) (x_1, \dots, x_i) ( x 1 , … , x i ) m i + 1 × ⋯ × m n m_{i+1} \times \dots \times m_n m i + 1 × ⋯ × m n 搜索目标 :
解空间树 回溯法解决问题的过程可以看作是在一个“解空间树”上进行搜索。
解空间 :满足显式约束 条件的所有元组构成的集合。这些元组是潜在的解。可行解 :解空间中满足隐式约束 条件的元组。解空间树 :将解空间中的元组以及它们的构造过程用树形结构表示出来。解空间树的结构 :树的根节点通常表示初始状态(例如一个空的部分解)。 树的内部节点表示正在构造中的部分解。 树的叶子节点通常表示一个完整的(可能但不一定满足所有隐式约束的)解。 问题状态 :解空间树中的所有节点 。解状态 :从根节点到解空间树中某个节点 X X X 显式约束 条件。也就是叶子结点的数目 。答案状态 :一个解状态节点 X X X 隐式约束 ,那么这个节点 X X X 对应的元组就是问题的一个解 。回溯法解决问题的过程就是在解空间树上搜索答案状态结点 的过程。
在回溯法搜索解空间树的过程中,树是动态生成的。
静态树 :指解空间树的完整结构 。这个结构在问题实例给定后理论上是确定的,与具体的问题实例无关 。动态树 :指在回溯搜索过程中,算法实际生成和访问过的那部分解空间树。树的节点是根据搜索的进展逐步生成的,与实例相关 。活结点 :一个已经被生成,但其所有子节点尚未全部生成的节点。E-结点 (Expanding Node):当前正在处理的活结点,算法正在尝试生成它的子节点。一个时刻通常只有一个 E-结点。死结点 :一个不再需要进一步扩展的节点。这可能是因为它所有的子节点都已经被生成和检查过了,或者是因为根据限界函数判断出从这个节点出发不可能找到解(或更好的解),于是被剪枝了 。在解空间树中如何选择下一个E-结点,即搜索策略,就涉及到问题状态的生成的相关问题。
第一种状态生成方法 (DFS):
当当前的E-结点 R R R C C C C C C 算法会沿着 C C C 只有当子树 C C C C C C R R R R R R R R R 这是回溯法通常采用的策略 。第二种状态生成方法 :
一个E-结点会一直保持为E-结点,直到它生成了它所有的子节点,然后它才变成死结点。接下来再从活结点列表中选择下一个E-结点。 组织活结点列表的方法有:BFS :如果活结点列表用队列 来管理(先进先出),那么节点是按层生成的。这对应的是分支限界法 的一种常见策略。D-检索生成法 :如果活结点列表用栈 来管理(后进先出),其效果类似于深度优先搜索。实际上,递归实现的回溯法隐式地使用了一个系统栈,行为就非常像 D-Search 或 DFS。 设计一个回溯算法通常遵循以下设计思想:
定义解空间树结构 :明确问题的解可以用什么形式的元组 来表示(固定长度还是可变长度)。 定义显式约束条件 (每个分量的取值范围)。 定义隐式约束条件 (分量之间或整体解需要满足的条件)。 检验问题满足多米诺性质 :思考并确认,如果一个部分解已经不满足某些条件,那么继续扩展它也无法得到有效解。这是设计有效限界函数的基础。 深度优先搜索 :以深度优先的方式遍历解空间树。这意味着算法会尽可能深地探索树的一条分支。 使用限界函数剪枝 :在搜索过程中,每扩展到一个新的节点(即构造出一个新的部分解),就使用限界函数进行判断。 如果限界函数表明从当前节点出发不可能得到问题的解(或者不可能得到比当前已找到的最优解更好的解),则不再继续扩展该节点(即剪枝),直接回溯。 具体步骤 :
从根节点开始,根节点成为第一个活结点,也是当前的扩展结点 (E-结点)。 沿着当前 E-结点向下(纵深方向)选择一个子节点,使其成为新的活结点和新的E-结点。 重复步骤 2 ,不断深入。 如果当前的E-结点不能再向纵深方向移动(即它没有未生成的子节点,或者所有子节点都被尝试过或剪枝了),那么这个E-结点就变成死结点。 此时,算法回溯 到该死结点的父节点(最近的一个活结点),并使该父节点成为新的E-结点,尝试扩展它的其他分支。 这个过程(深入、遇到死胡同、回溯、尝试其他路)一直持续,直到找到所要求的解(一个、所有或最优),或者整个解空间树中已没有活结点(意味着所有可能性都已探索完毕)。 回溯法效率分析 回溯算法解决组合问题时,效率受多个因素影响,包括:
生成下一个 X ( k ) X(k) X ( k ) 生成一个结点的时间
满足显式约束条件的 X ( k ) X(k) X ( k ) 子结点的数量
限界函数 B i B_i B i 检验结点的时间
对所有 i i i B i B_i B i X ( k ) X(k) X ( k ) 通过检验的结点数量
回溯算法的解空间可能非常大:
如子集问题,解空间为 2 n 2^n 2 n 如排列问题,解空间为 n ! n! n ! 所以回溯法在最坏情况下时间复杂度 为: O ( p ( n ) ⋅ 2 n ) O(p(n) \cdot 2^n) O ( p ( n ) ⋅ 2 n ) O ( q ( n ) ⋅ n ! ) O(q(n) \cdot n!) O ( q ( n ) ⋅ n !) p ( n ) , q ( n ) p(n), q(n) p ( n ) , q ( n )
但在实际中,很多实例的剪枝效果很好 ,导致实际运行非常快。
蒙特卡罗方法 蒙特卡罗方法的核心思想是:
假定限界函数固定 随机走一条路径(每层随机选择一个未被限界的子结点) 记录这条路径中每层的子结点数 m 1 , m 2 , m 3 , … m_1, m_2, m_3, \dots m 1 , m 2 , m 3 , … 推导出树上大致结点数 估计为: m = 1 + m 1 + m 1 ⋅ m 2 + m 1 ⋅ m 2 ⋅ m 3 + ⋯ m = 1 + m_1 + m_1 \cdot m_2 + m_1 \cdot m_2 \cdot m_3 + \cdots m = 1 + m 1 + m 1 ⋅ m 2 + m 1 ⋅ m 2 ⋅ m 3 + ⋯
m i m_i m i i i i 平均没受限界 的儿子结点数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def estimate (root, generate_children, bound_function ):""" 使用蒙特卡罗方法估算状态树中未被限界的结点总数 参数: - root: 根节点的状态 - generate_children(state): 返回所有可能的子状态列表 - bound_function(state): 判断某个状态是否被限界(返回 True 表示通过限界) 返回: - m: 估算的未被限界结点总数 """ 1 1 1 while True :for child in generate_children(state) if bound_function(child)]if not children:break len (children)1 return m
graph TD
A[根结点X1] --> B1[X2_1]
A --> B2[X2_2]
A --> B3[X2_3]
B1 --> C1[X3_1]
B1 --> C2[X3_2]
B2 --> C3[X3_3]
B3 --> C4[X3_4]
B3 --> C5[X3_5]
C1 --> D1[X4_1]
C1 --> D2[X4_2]
%% 随机选择路径:A → B1 → C1 → D1
click A call showMessage("被选中路径:A")
click B1 call showMessage("被选中路径:A->B1")
click C1 call showMessage("被选中路径:A->B1->C1")
click D1 call showMessage("被选中路径:A->B1->C1->D1")
style A fill:#aaffaa,stroke:#333,stroke-width:2px
style B1 fill:#aaffaa,stroke:#333,stroke-width:2px
style C1 fill:#aaffaa,stroke:#333,stroke-width:2px
style D1 fill:#aaffaa,stroke:#333,stroke-width:2px
蒙特卡罗方法的特点:
优点:
适用于估算整个状态空间中的结点数 ,例如 N N N 限界函数固定 时,每层同样处理,简单高效,如果需要用到估值等方法,那么效率会很低很低缺点:
只求一个解时不够精确,它是从统计角度去实现的,并不擅长于找一个解 蒙特卡罗方法使用一个固定的限界函数 ,但在现实中随着状态的推进,对哪些路径有希望其实知道得越来越多,如果限界函数不随状态推进而动态增强 ,就会导致仍然尝试很多其实没希望的路径,使得估计值 m m m 子集和问题 给定一组不同的正整数 W = ( w 1 , w 2 , … , w n ) W = (w_1, w_2, \dots, w_n) W = ( w 1 , w 2 , … , w n ) M M M M M M
输入 :正整数数组 W ( 1 : n ) W(1:n) W ( 1 : n ) M M M
输出 :所有满足 ∑ i = 1 n w i x i = M \sum_{i=1}^n w_i x_i = M ∑ i = 1 n w i x i = M n n n X = ( x 1 , … , x n ) X = (x_1,\dots,x_n) X = ( x 1 , … , x n ) x i ∈ { 0 , 1 } x_i \in \{0,1\} x i ∈ { 0 , 1 }
x i = 1 x_i = 1 x i = 1 w i w_i w i x i = 0 x_i = 0 x i = 0 w i w_i w i 解空间建模 :
每一个解可表示为一个 n n n X = ( x 1 , x 2 , … , x n ) X = (x_1, x_2, \dots, x_n) X = ( x 1 , x 2 , … , x n ) x i ∈ { 0 , 1 } x_i \in \{0,1\} x i ∈ { 0 , 1 } 总的解空间大小为 2 n 2^n 2 n 显式约束:每个 x i ∈ { 0 , 1 } x_i \in \{0,1\} x i ∈ { 0 , 1 } 隐式约束 :当前选择的元素之和必须恰好为 M M M 限界函数 :
设:
当前考虑到第 k k k x 1 , x 2 , … , x k − 1 x_1, x_2, \dots, x_{k-1} x 1 , x 2 , … , x k − 1 s = ∑ i = 1 k − 1 w i x i s = \sum_{i=1}^{k-1} w_i x_i s = ∑ i = 1 k − 1 w i x i r = ∑ i = k n w i r = \sum_{i=k}^{n} w_i r = ∑ i = k n w i 必要条件 : s + r ≥ M s + r \geq M s + r ≥ M M M M
上限条件 : s + w k ≤ M s + w_k \leq M s + w k ≤ M
若不对 W W W 排序 :
无法有效判断下一步是否可能超过 M M M 会导致大量冗余搜索,剪枝效果大打折扣 效率从近线性下降为指数级增加 ,搜索树接近完整 2 n 2^n 2 n 子集和问题最坏时间复杂度 O ( 2 n ) O(2^n) O ( 2 n )
例子:n = 4 , ( w 1 , w 2 , w 3 , w 4 ) = ( 11 , 13 , 24 , 7 ) , M = 31 n=4, (w_1, w_2, w_3, w_4) = (11, 13, 24, 7), M=31 n = 4 , ( w 1 , w 2 , w 3 , w 4 ) = ( 11 , 13 , 24 , 7 ) , M = 31
可行解1:{ 11 , 13 , 7 } \{11, 13, 7\} { 11 , 13 , 7 } { 24 , 7 } \{24, 7\} { 24 , 7 }
1. 固定长元组表达
元组形式:( x 1 , x 2 , x 3 , x 4 ) (x_1, x_2, x_3, x_4) ( x 1 , x 2 , x 3 , x 4 )
可行解1:( 1 , 1 , 0 , 1 ) (1, 1, 0, 1) ( 1 , 1 , 0 , 1 ) 11 ⋅ 1 + 13 ⋅ 1 + 24 ⋅ 0 + 7 ⋅ 1 = 11 + 13 + 7 = 31 11 \cdot 1 + 13 \cdot 1 + 24 \cdot 0 + 7 \cdot 1 = 11+13+7 = 31 11 ⋅ 1 + 13 ⋅ 1 + 24 ⋅ 0 + 7 ⋅ 1 = 11 + 13 + 7 = 31
可行解2:( 0 , 0 , 1 , 1 ) (0, 0, 1, 1) ( 0 , 0 , 1 , 1 ) 11 ⋅ 0 + 13 ⋅ 0 + 24 ⋅ 1 + 7 ⋅ 1 = 24 + 7 = 31 11 \cdot 0 + 13 \cdot 0 + 24 \cdot 1 + 7 \cdot 1 = 24+7 = 31 11 ⋅ 0 + 13 ⋅ 0 + 24 ⋅ 1 + 7 ⋅ 1 = 24 + 7 = 31
显式约束:x i ∈ 0 , 1 x_i \in {0, 1} x i ∈ 0 , 1 i = 1 , 2 , 3 , 4 i=1,2,3,4 i = 1 , 2 , 3 , 4
隐式约束:11 x 1 + 13 x 2 + 24 x 3 + 7 x 4 = 31 11x_1 + 13x_2 + 24x_3 + 7x_4 = 31 11 x 1 + 13 x 2 + 24 x 3 + 7 x 4 = 31
多米诺性质:如果当前部分和 ∑ w i x i M \sum w_i x_i \> M ∑ w i x i M
解空间大小:2 4 = 16 2^4 = 16 2 4 = 16
子集和问题的4-元组表达的解空间树 (这是一个二叉树,每个节点代表对一个 w i w_i w i
问题状态 :树中的所有节点(包括中间节点和叶节点)。对于一个深度为4的完整二叉树,节点总数是 2 n + 1 − 1 = 2 5 − 1 = 31 2^{n+1}-1 = 2^5-1 = 31 2 n + 1 − 1 = 2 5 − 1 = 31 解状态 :所有叶节点(共 2 4 = 16 2^4 = 16 2 4 = 16 答案状态 :在16个叶节点中,满足隐式约束 ∑ w i x i = M \sum w_i x_i = M ∑ w i x i = M 2. 可变长元组表达
元组形式:( x 1 , … , x k ) (x_1, \dots, x_k) ( x 1 , … , x k ) x i x_i x i x 1 < x 2 < ⋯ < x k x_1 < x_2 < \dots < x_k x 1 < x 2 < ⋯ < x k
可行解1:( 1 , 2 , 4 ) (1, 2, 4) ( 1 , 2 , 4 ) w 1 , w 2 , w 4 w_1, w_2, w_4 w 1 , w 2 , w 4
可行解2:( 3 , 4 ) (3, 4) ( 3 , 4 ) w 3 , w 4 w_3, w_4 w 3 , w 4
显式约束:x i ∈ 1 , 2 , 3 , 4 x_i \in {1, 2, 3, 4} x i ∈ 1 , 2 , 3 , 4 x 1 < x 2 < ⋯ < x k x_1 < x_2 < \dots < x_k x 1 < x 2 < ⋯ < x k
隐式约束:∑ j = 1 k w x j = M \sum_{j=1}^{k} w_{x_j} = M ∑ j = 1 k w x j = M
多米诺性质:同上,如果当前部分和已大于 M M M
解空间大小:所有可能的子集个数,即 2 n = 16 2^n = 16 2 n = 16
子集和问题的 n = 4 n=4 n = 4 k k k
问题状态 :树中的所有节点。解状态 :树中的所有节点都可以看作一个(部分或完整的)解状态,因为它们都代表了一个合法的子集(满足显式约束,即元素不重复且有序)。答案状态 :在所有节点中,其路径代表的子集元素之和等于 M M M 八皇后问题 ∀ n ≥ 4 \forall n\ge 4 ∀ n ≥ 4 n n n
在一个 n × n n×n n × n n n n 互不攻击 :
解的表示形式 :一个 n n n ( x 1 , x 2 , … , x n ) (x₁, x₂, \dots, xₙ) ( x 1 , x 2 , … , x n ) x i xᵢ x i i i i x i xᵢ x i
显式约束条件 (变量范围):
每个皇后只能在某一列:x i ∈ { 1 , 2 , … , n } , 1 ≤ i ≤ n x_i \in \{1, 2, \dots, n\}, 1 \le i \le n x i ∈ { 1 , 2 , … , n } , 1 ≤ i ≤ n 所有组合形成一个 n n n^n n n 隐式约束条件 (合法解筛选):
所有 x i x_i x i 不在同一对角线,即满足:∣ x i − x j ∣ ≠ ∣ i − j ∣ |x_i - x_j| \ne |i - j| ∣ x i − x j ∣ = ∣ i − j ∣ 可通过判断 ( i − x i ) ≠ ( j − x j ) (i - x_i) \ne (j - x_j) ( i − x i ) = ( j − x j ) ( i + x i ) ≠ ( j + x j ) (i + x_i) \ne (j + x_j) ( i + x i ) = ( j + x j )
满足隐式约束的才是合法解,则解空间缩小为 n ! n! n !
状态空间树 结构:
每层表示一个皇后的放置(即第 k k k 每个结点表示当前行皇后放在某列 树的路径 ( x 1 , x 2 , … , x k ) (x_1, x_2, \dots, x_k) ( x 1 , x 2 , … , x k ) k k k 解空间遍历策略 (回溯):
类似 DFS,递归深入每一层 使用限界函数(PLACE ( k ) \text{PLACE}(k) PLACE ( k ) 如果冲突,则跳过/回溯到上一层 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 procedure PLACE(k)
效率估计 状态空间总规模:
原始空间(不剪枝):1 + n + n 2 + ⋯ + n n 1 + n + n^2 + \dots + n^n 1 + n + n 2 + ⋯ + n n 排除列冲突(每列仅用一次):n ! n! n ! 8 皇后状态树结点数约为 69281(即最多访问这么多结点) 使用限界函数后:
最坏情况下八皇后问题复杂度为 O ( n ! ) O(n!) O ( n !)
图着色问题 给定一个无向图 G = ( V , E ) G=(V,E) G = ( V , E ) v ∈ V v \in V v ∈ V 任何两个相邻的顶点颜色不同 。给定 m m m
解向量表示 :用一个 n n n X = ( x 1 , x 2 , … , x n ) X = (x_1, x_2, \dots, x_n) X = ( x 1 , x 2 , … , x n ) x i x_i x i i i i 1 ≤ x i ≤ m 1 \leq x_i \leq m 1 ≤ x i ≤ m
显式约束 : x i ∈ [ 1 , m ] x_i\in [1,m] x i ∈ [ 1 , m ]
隐式约束 :如果 ⟨ i , j ⟩ ∈ E \langle i,j\rangle\in E ⟨ i , j ⟩ ∈ E x i ≠ x j x_i \ne x_j x i = x j
整个问题可以看成是在一个 m n m^n m n 完全 m m m 中搜索满足条件的解。
用回溯法解决 3 个顶点的 3 种颜色的图着色问题,在最坏情况下将生成 ? 个结点?
n n n m m m m m m m m m n n n
3 个顶点,3 种颜色,所以共有 1 + 3 + 3 × 3 + 3 × 3 × 3 = 40 1+3+3\times3+3\times3\times3=\boxed{40} 1 + 3 + 3 × 3 + 3 × 3 × 3 = 40
限界函数 OK(k):判断当前顶点 k k k
1 2 3 4 5 procedure OK(k)
回溯求解 m m m
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 procedure MCOLORING(V,E,C,n,m)
最坏情况时间复杂度是 O ( m n ) O(m^n) O ( m n )
分支限界法 分支限界法是一种系统地搜索问题解空间树 的算法,常用于组合优化问题 。适用问题特点:
解空间庞大(组合问题) 需要找到最优解 有“剪枝”条件(约束函数) 可用元组表示解 回溯法 分支限界法 目标 找到一个或全部可行解 找到最优解 剪枝依据 可行性 可行性 + 最优性 (使用成本估计函数)活结点选择方式(主要区别) 深度优先 按策略选择 (队列/优先队列)选择子节点 如何选下一个扩展结点 E E E 更聪明的选择:如选代价最小的活结点(LC)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 Procedure BB(T)
活结点表的管理方式 :
FIFO 检索 (BFS):
活结点按“生成顺序”处理
使用队列
对于找“某个”解较快,但不是最优解
LC 检索 (Least Cost,优先队列):
成本函数 使用成本函数 c ( X ) c(X) c ( X ) 赋以优先次序 ,其定义关注最小成本:
基于 X X X 寻找生成最小数目的答案结点 基于距离 X X X 寻找路径长度最短的答案结点 基于问题描述中的目标函数定义,寻找使目标函数取极值的答案节点 如果不存在目标函数定义,那么一般采用方法 2。
用 cost(X) \text{cost(X)} cost(X) 答案结点 X X X X X X c ( X ) c(X) c ( X )
c ( X ) = { cost(X) X 是答案结点 min { cost ( P ) ∣ 答案结点 P ∈ 子树 X } 子树 X 中包含答案结点 ∞ 子树 X 不包含答案结点 c(X)= \begin{cases} \text{cost(X)} && X\text{ 是答案结点}\\ \min\{\text{cost}(P)\mid\text{答案结点} P \in \text{子树} X\} && \text{子树} X \text{中包含答案结点}\\ \infty && \text{子树} X \text{不包含答案结点}\\ \end{cases} c ( X ) = ⎩ ⎨ ⎧ cost(X) min { cost ( P ) ∣ 答案结点 P ∈ 子树 X } ∞ X 是答案结点 子树 X 中包含答案结点 子树 X 不包含答案结点
但是要得到函数 c c c
c ( X ) c(X) c ( X ) c ( X ) c(X) c ( X ) 基于 c c c 成本估计函数 c ^ \hat{c} c ^ c c c
定义c ^ ( X ) \hat{c}(X) c ^ ( X )
明确根到 X X X 估计 X X X 项目 说明 成本函数 c ( X ) {c}(X) c ( X ) 真正的最优代价(很难求) 估计函数 c ^ ( X ) \hat{c}(X) c ^ ( X ) 对 c ( X ) c(X) c ( X )
需要满足: c ^ ( X ) ≤ c ( X ) \hat{c}(X) \le c(X) c ^ ( X ) ≤ c ( X ) X X X c ^ ( X ) = c ( X ) \hat{c}(X) = c(X) c ^ ( X ) = c ( X )
c ^ \hat{c} c ^
c ^ ( X ) = h ( X ) + g ^ ( X ) \hat{c}(X) = h(X) + \hat{g}(X) c ^ ( X ) = h ( X ) + g ^ ( X )
其中:
h ( X ) h(X) h ( X ) X X X g ^ ( X ) \hat{g}(X) g ^ ( X ) X X X 最小成本答案结点 的估计代价(设计的关键)例如,旅行商问题中,h ( X ) h(X) h ( X ) g ^ ( X ) \hat{g}(X) g ^ ( X )
LC 检索过程 LC 检索使用 优先队列 ,每次扩展估计总代价 c ^ ( X ) \hat{c}(X) c ^ ( X ) 最小 的活结点。
初始化优先队列(根结点入队,f = 0 f=0 f = 0 g ^ \hat{g} g ^
重复以下操作直到找到目标状态:
若队列空了还没找到,说明无解
BFS 就是 LC 检索过程中, g ^ ( X ) = 0 \hat{g}(X)=0 g ^ ( X ) = 0
LC 检索适用于求解最优解问题。
15-谜问题 给定一个 4 × 4 4×4 4 × 4
1 2 3 4 1 2 3 4
状态空间树的建模 :
结点表示一个棋牌布局状态 边表示一次合法移动 (即空格向上、右、下、左移动一次)初始状态是根结点,目标状态是一个特定的叶结点。 每个状态最多有 4 个子结点(根据空格能移动的方向) 可达性判定定理
按下图方式编号:
1 2 3 4 1 2 3 4
POSITION ( i ) \text{POSITION}(i) POSITION ( i ) i i i
LESS ( i ) \text{LESS}(i) LESS ( i ) i i i j j j POSITION ( j ) > POSITION ( i ) \text{POSITION}(j) > \text{POSITION}(i) POSITION ( j ) > POSITION ( i )
例如,如果牌 5 在第 2 行,但 1~4 中有两个排在它之后,那 LESS ( 5 ) = 2 \text{LESS}(5)=2 LESS ( 5 ) = 2
X X X 设总逆序数为 S = ∑ LESS( i ) S = \sum \text{LESS(}i) S = ∑ LESS( i ) 若 S + X S + X S + X 。
如果使用深度优先搜索或 FIFO 检索,效率不高:
定义 c ( X ) c(X) c ( X )
基于 c ( X ) c(X) c ( X ) 启发式 的估价函数 c ^ \hat{c} c ^
c ^ ( X ) = f ( X ) + g ^ ( X ) \hat{c}(X) = f(X) + \hat{g}(X) c ^ ( X ) = f ( X ) + g ^ ( X )
1 2 3 4 1 2 3 4
计算逆序对数 LESS ( i ) \text{LESS}(i) LESS ( i ) LESS ( 15 ) = 1 \text{LESS}(15) = 1 LESS ( 15 ) = 1 LESS ( 14 ) = 1 \text{LESS}(14) = 1 LESS ( 14 ) = 1 0 0 0 ∑ LESS ( i ) = 2 \sum \text{LESS}(i)=2 ∑ LESS ( i ) = 2 空格在第 4 行 (X = 4 X=4 X = 4 所以:S + X = 2 + 4 = 6 S + X = 2 + 4 = 6 S + X = 2 + 4 = 6 2 ∣ 6 2|6 2∣6 是可达状态 。
求最小成本的分支限界法 很多组合优化问题不仅需要找到可行解 ,而且要找出具有最小代价或最大收益的最优解 。这类问题可以建模为在解空间树 中搜索具有最小成本的答案结点 。
先前的算法中:算法一旦判断出儿子结点 X X X 并不一定能得到最优解 。
因为估计函数 c ^ ( X ) \hat c (X) c ^ ( X )
∀ X , Y , if c ( X ) < c ( Y ) s.t. c ^ ( X ) < c ^ ( Y ) \forall X, Y,\text{if } c(X)<c(Y) \text{ s.t. } \hat c(X)< \hat c(Y) ∀ X , Y , if c ( X ) < c ( Y ) s.t. c ^ ( X ) < c ^ ( Y )
那么估计函数现在需要满足的条件有:
易于计算 c ^ ( X ) ≤ c ( X ) \hat{c}(X) \le c(X) c ^ ( X ) ≤ c ( X ) X X X c ^ ( X ) = c ( X ) \hat{c}(X) = c(X) c ^ ( X ) = c ( X ) X X X c ^ ( X ) < c ^ ( Y ) \hat{c}(X) < \hat{c}(Y) c ^ ( X ) < c ^ ( Y ) c ( X ) < c ( Y ) c(X) < c(Y) c ( X ) < c ( Y ) 前三条是必要条件,第四条是附加条件。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 procedure LC(T, ĉ)
在算法 LC 中,我们得到的一定是成本最小的解:
对于活结点表中的每一个结点 L L L c ^ ( E ) ≤ c ^ ( L ) \hat c(E)\le \hat c(L) c ^ ( E ) ≤ c ^ ( L ) c ^ \hat c c ^ E E E c ( E ) = c ^ ( E ) c(E)=\hat c(E) c ( E ) = c ^ ( E ) c ( E ) = c ^ ( E ) ≤ c ^ ( L ) ≤ c ( L ) c(E)=\hat c(E)\le\hat c(L)\le c(L) c ( E ) = c ^ ( E ) ≤ c ^ ( L ) ≤ c ( L ) 因此,算法 LC 选中的是成本最小的答案结点 若答案结点 E E E c ^ ( E ) = c ( E ) \hat c(E)=c(E) c ^ ( E ) = c ( E ) 算法 LC 也不能给出成本最小的答案结点 。
加速寻找最小成本 为加速搜索并减少无效分支扩展 ,引入最小成本上界 U U U U U U 答案结点的最小成本 。
在一开始 U = ∞ U=\infty U = ∞ 最小成本答案结点的成本给它赋值 。它会随着结点的访问不断改小。
U U U 界定当前结点的死活,并通过剪枝加快找到最优解 。如果某个结点的估计值 c ^ ( X ) ≥ U \hat{c}(X) \ge U c ^ ( X ) ≥ U X X X 不可能产生更优解 ,可以剪枝。
为提高 U U U U U U U U U 成本上界函数 u ( X ) u(X) u ( X ) c ( X ) c(X) c ( X )
易于计算 c ( X ) ≤ u ( X ) c(X)\le u(X) c ( X ) ≤ u ( X ) 当叶结点 X X X c ( X ) = u ( X ) c(X)=u(X) c ( X ) = u ( X ) 对于结点 X X X c ^ ( X ) ≤ c ( X ) ≤ u ( X ) \hat c(X)\le c(X)\le u(X) c ^ ( X ) ≤ c ( X ) ≤ u ( X )
可以看出, c ^ ( X ) \hat c(X) c ^ ( X ) u ( X ) u(X) u ( X ) 子树 X X X 所有答案结点成本最小值 c ( X ) c(X) c ( X )
c ^ ( X ) < c ( X ) < u ( X ) \hat c(X)<c(X)<u(X) c ^ ( X ) < c ( X ) < u ( X )
算法在生成状态结点时,当 X X X cost ( X ) < U \text{cost}(X)<U cost ( X ) < U 改小 U U U
发现一个答案结点 X X X cost ( X ) \text{cost}(X) cost ( X ) U U U 发现一个状态结点 X X X u ( X ) u(X) u ( X ) U U U 接下来就可以根据 U U U
若 U U U c ^ ( X ) ≥ U \hat c(X)\textcolor{red}{\ge} U c ^ ( X ) ≥ U X X X U U U 若 U U U c ^ ( X ) > U \hat c(X)\textcolor{red}{>} U c ^ ( X ) > U X X X U U U 如果答案结点 X X X cost ( X ) \text{cost}(X) cost ( X ) u ( X ) u(X) u ( X ) U U U
像上面说的一样, U U U 剪枝策略会不同 ,那么为方便剪枝,当 U U U u ( X ) u(X) u ( X ) U U U
定义一个足够小的正常数 ϵ \epsilon ϵ X , Y X, Y X , Y u ( X ) < u ( Y ) u(X)<u(Y) u ( X ) < u ( Y ) u ( X ) < u ( X ) + ϵ < u ( Y ) u(X)<u(X)+\epsilon<u(Y) u ( X ) < u ( X ) + ϵ < u ( Y )
当 U U U u ( X ) u(X) u ( X ) 追加 一个 ϵ \epsilon ϵ U ← u ( X ) + ϵ U\leftarrow u(X)+\epsilon U ← u ( X ) + ϵ 当 U U U cost ( X ) \text{cost}(X) cost ( X ) U ← cost ( X ) U\leftarrow\text{cost}(X) U ← cost ( X ) 改进后的 U U U X X X c ^ ( X ) ≤ U \hat c(X)\le U c ^ ( X ) ≤ U X X X
改进后的最小成本 BB :使用上下界。定义函数 UB ( X , ϵ , U , a n s ) \text{UB}(X, \epsilon, U, ans) UB ( X , ϵ , U , an s )
1 2 3 4 5 6 7 8 9 10 11 if ĉ(X) ≥ U:
cost ( X ) \text{cost}(X) cost ( X ) u ( X ) u(X) u ( X ) c ( X ) ≤ u ( X ) c(X) \le u(X) c ( X ) ≤ u ( X ) ϵ \epsilon ϵ 下面是一些完整算法示例:
FIFO 分支限界算法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 FIFOBB(T, ĉ, u, ε, cost)
LC 分支限界算法 ,用最小堆维护活结点表,始终扩展 c ^ \hat{c} c ^ 1 2 3 4 5 6 7 8 9 10 11 12 LCBB(T, ĉ, u, ε, cost)
遇到极大化问题如何处理?
反转目标函数 ,把目标函数 f ( X ) f(X) f ( X ) − f ( X ) -f(X) − f ( X ) 镜像修改问题 ,成本函数仍为 c ( X ) = f ( X ) c(X)=f(X) c ( X ) = f ( X ) c ^ ( X ) \hat{c}(X) c ^ ( X ) u ( X ) u(X) u ( X ) u ( X ) ≤ c ( X ) ≤ c ^ ( X ) u(X) \le c(X) \le \hat{c}(X) u ( X ) ≤ c ( X ) ≤ c ^ ( X ) 核心机制 组成部分 作用 B ( X ) B(X) B ( X ) 剪掉不可行结点 c ^ ( X ) \hat{c}(X) c ^ ( X ) 估算最小可能成本,辅助排序/剪枝 u ( X ) u(X) u ( X ) 推动上界 U U U U U U 当前已知最优解的成本,界定活/死结点 ϵ \epsilon ϵ 防止浮点误差或相等值比较中的剪枝失误
带有期限的作业调度问题 有一台机器和 n n n i i i ( p i , d i , t i ) (p_i, d_i, t_i) ( p i , d i , t i )
p i p_i p i d i d_i d i t i t_i t i 目标:从中选择一个子集 J J J 按顺序安排在机器上,且都能在各自截止时间前完成 ,剩下那些不能完成的作业,求它们的总罚款最小(极小化罚款总数)。
解空间表示:
用不定长的 k k k ( X 1 , X 2 , … , X k ) (X_1, X_2, \dots, X_k) ( X 1 , X 2 , … , X k ) 显式约束 : X i ≤ X i + 1 X_i \le X_{i+1} X i ≤ X i + 1 隐式约束 :这些作业必须能在各自的 d i d_i d i 成本估计函数 c ^ ( X ) \hat{c}(X) c ^ ( X )
定义一个 乐观估计 (小于等于真实罚款),以指导分支限界法。 令 S x Sx S x X X X 定义 m = max { i ∈ S x } m = \max\{i \in S_x\} m = max { i ∈ S x } 如果 X X X c ^ ( X ) = ∑ p i , i < m 且 i ∉ S x \hat{c}(X) = \sum p_i, i<m \text{且} i \notin S_x c ^ ( X ) = ∑ p i , i < m 且 i ∈ / S x 如果 X X X c ^ ( X ) = ∞ \hat{c}(X) = \infty c ^ ( X ) = ∞ 定义 u ( X ) = ∑ p i , i ∉ S x u(X) = \sum p_i, i\notin S_x u ( X ) = ∑ p i , i ∈ / S x
初始时 U U U 若某个结点的估值 c ^ ( X ) ≥ 当前最优 U \hat{c}(X) \ge \text{当前最优} U c ^ ( X ) ≥ 当前最优 U 由于只有在叶子节点才能得到真正的罚款值 c ( X ) = c ^ ( X ) c(X) = \hat{c}(X) c ( X ) = c ^ ( X ) LC(最小成本优先)策略并不适用 ,应使用:
FIFO + 剪枝(BB-FIFO) LCBB(成本限界+最小估价)
0/1 背包问题的分支限界法解 解空间 :
每个结点是 n n n ( x 1 , x 2 , … , x n ) (x_1, x_2, \dots, x_n) ( x 1 , x 2 , … , x n ) 状态树中每个结点表示当前选与不选的路径。 共 2 n 2^n 2 n 可以用贪心解辅助估价 :物品按单位效益 p i / w i p_i/w_i p i / w i
对于物品 k + 1 k+1 k + 1 n n n 最后一个可能放部分,定义 Δ \Delta Δ 贪心解估价 = 当前收益 p + 额外可放收益 p p + Δ p j \text{贪心解估价} = \text{当前收益 } p + \text{ 额外可放收益 } pp + \Delta p_j 贪心解估价 = 当前收益 p + 额外可放收益 pp + Δ p j 关于成本估计函数 c ^ ( X ) \hat{c}(X) c ^ ( X ) u ( X ) u(X) u ( X )
p = ∑ p i x i p = \sum p_i x_i p = ∑ p i x i p p = ∑ p i pp = \sum p_i pp = ∑ p i Δ p j \Delta p_j Δ p j 那么:
成本估计函数:c ^ ( X ) = p + p p + Δ p j \hat{c}(X) = p + pp + \Delta p_j c ^ ( X ) = p + pp + Δ p j 成本下界函数:u ( X ) = p + p p u(X) = p + pp u ( X ) = p + pp 三者关系:
u ( X ) ≤ c ( X ) ≤ c ^ ( X ) u(X) \le c(X) \le \hat{c}(X) u ( X ) ≤ c ( X ) ≤ c ^ ( X )
X X X
约束函数 B B B
若当前路径选中的物品重量 > M \text{当前路径选中的物品重量} > M 当前路径选中的物品重量 > M 回溯和分支限界总结 状态空间生成方式 回溯法: 当前的 E-结点 R R R C C C C C C C C C R R R 分支限界法:当前结点一旦成为 E-结点,就一直处理到变成死结点为止。其生成的儿子结点加入到活结点表中,然后再从活结点表中选择下一个新的 E-结点。 基本思想对比 回溯法从根结点出发,按深度优先策略搜索解空间树。判断 E-结点是否包含问题的解。如果不包含,则跳过以该结点为根的子树,逐层向其祖先结点回溯。否则就进入该子树,继续按深度优先的策略进行搜索。 分支限界法从根结点出发,生成当前 E-结点全部儿子之后,再选择新的活结点成为 E-结点,重复上述过程。为提高算法效率,会使用限界函数和成本估计函数等进行剪枝。 NP-完全问题 什么是“好算法” 运行时间 是评价算法优劣的重要标准。一般来说,运行时间越短越好 。 不同算法处理同一问题,解决的问题规模 (n n n 多项式时间算法 时间复杂度为 O ( n k ) O(n^k) O ( n k ) O ( 1 ) O(1) O ( 1 ) O ( log n ) O(\log n) O ( log n ) O ( n ) O(n) O ( n ) O ( n log n ) O(n \log n) O ( n log n ) O ( n 2 ) O(n^2) O ( n 2 ) 可接受或高效 ,属于 P 类问题 。
非多项式时间算法 (指数级)时间复杂度如 O ( 2 n ) O(2^n) O ( 2 n ) O ( n ! ) O(n!) O ( n !) O ( n n ) O(n^n) O ( n n ) 不可接受 ”的算法。
算法复杂性 指的是某个特定算法的执行时间 ,例如冒泡排序是 O ( n 2 ) O(n^2) O ( n 2 )
问题复杂性 是解决某类问题所需的最优算法的时间复杂度 ,例如排序问题的复杂性是 O ( n log n ) O(n \log n) O ( n log n )
现实问题类型 描述与例子 多项式级问题 有高效算法,例如排序、最小生成树、最短路径 不可计算问题 根本无法求解,如希尔伯特第十问题 指数级问题 已证明无多项式解,例如带幂的正则表达式 未确定多项式级问题 目前没有找到多项式解,且尚未证明不存在,如图着色、TSP、0/1背包、最大团等
优化问题与判定问题 :
优化问题 :求最优解,如最大值/最小值。判定问题 :只需回答“是/否”。优化问题 ⇄ 判定问题 是可相互转化的 。若判定问题可多项式求解 ⇔ 优化问题也可。
优化 → 判定:直接比较最优解与 k k k 判定 → 优化:不断尝试 k = n , n − 1 , … k = n, n-1, \dots k = n , n − 1 , … k k k 将优化问题转为判定问题有利于输出统一(是/否),便于分类、比较和复杂性分析,也是进行 NP 复杂性分类 的基础。
不确定的判定问题 与确定性算法不同,不确定算法允许存在猜测 ,并允许choice(S) 函数,从 S 中瞬间猜中 答案。
1 2 3 choice(S)
choice(S) 是一种“魔法选择”,总能选中正确解。
这种能力存在于理论模型“不确定机 ”中,是 NP 概念的基础。
不确定算法的结构是:
猜测阶段 (非确定阶段),用 choice() 猜一个潜在的解。验证阶段 (确定阶段),检查猜测是否正确。验证阶段的时间复杂度必须是多项式级 ,所以 整体算法时间复杂度 = 猜测 + 验证 = O ( 多项式 ) 整体算法时间复杂度 = 猜测 + 验证 = O(多项式) 整体算法时间复杂度 = 猜测 + 验证 = O ( 多项式 ) 为了统一度量不同判定问题的算法时间复杂度,不同算法的输入参数均转换为二进制形式,算法时间复杂度基于二进制输入长度 来考虑。
例如最大团问题中图 G G G
m = n 2 + ⌊ log 2 k ⌋ + ⌊ log 2 n ⌋ + 2 m = n^2 + \lfloor \log_2 k\rfloor + \lfloor\log_2n\rfloor + 2 m = n 2 + ⌊ log 2 k ⌋ + ⌊ log 2 n ⌋ + 2
分别每一项对应邻接矩阵,待判定的结点数,结点数。
则最大团判定方法 DCK ( G , n , k ) \text{DCK}(G, n, k) DCK ( G , n , k ) O ( n 2 ) = O ( m ) O(n^2)=O(m) O ( n 2 ) = O ( m )
P 问题和 NP 问题 P 问题 (Polynomial-time problems)指能在多项式时间内由确定性算法(即普通程序)解决 的判定问题集合。即:
P = { L ∣ 存在多项式时间算法 A,使得 ∀ x , A ( x ) 能在多项式时间内判定 x ∈ L } \mathbf{P} = \{ L \mid \text{存在多项式时间算法 A,使得 } \forall x, A(x) \text{ 能在多项式时间内判定 } x \in L \} P = { L ∣ 存在多项式时间算法 A ,使得 ∀ x , A ( x ) 能在多项式时间内判定 x ∈ L }
NP 问题 (Nondeterministic Polynomial-time problems)指可以在多项式时间内由不确定算法“猜测”并“验证”解是否成立 的问题集合。
也就是说,对于一个 NP 问题,我们可以在多项式时间内验证一个候选解是否正确 。
P ⊆ N P \mathbf{P} \subseteq \mathbf{NP} P ⊆ NP
目前仍然无法证明 P = N P \mathbf{P = NP} P = NP P ≠ N P \mathbf{P \ne NP} P = NP
归约 归约是一种在研究问题之间难度关系时使用的转换方式。
L 1 L_1 L 1 L 2 L_2 L 2 L 1 ≤ L 2 L_1 \leq L_2 L 1 ≤ L 2 L 1 ∝ L 2 L_1 \propto L_2 L 1 ∝ L 2 转换函数 T ( x ) T(x) T ( x ) ∀ x \forall x ∀ x x ∈ L 1 ⟺ T ( x ) ∈ L 2 x \in L_1 \iff T(x) \in L_2 x ∈ L 1 ⟺ T ( x ) ∈ L 2 L 2 L_2 L 2 L 1 L_1 L 1
如果 L 1 ≤ L 2 L_1 \leq L_2 L 1 ≤ L 2 L 1 L_1 L 1 L 2 L_2 L 2
归约具有传递性 :若 L 1 ≤ L 2 L_1 \leq L_2 L 1 ≤ L 2 L 2 ≤ L 3 L_2 \leq L_3 L 2 ≤ L 3 L 1 ≤ L 3 L_1 \leq L_3 L 1 ≤ L 3
若归约函数 T T T 多项式时间归约 ,记为:
L 1 ≤ p L 2 L_1 \leq_p L_2 L 1 ≤ p L 2
如果 L 2 L_2 L 2 L 1 L_1 L 1 反之,如果 L 1 L_1 L 1 L 2 L_2 L 2 一般而言,规约都需要的是多项式规约。如果一个“规约”是超多项式规约的,那么两个问题就不能够比较它们的难度了,因为规约难度就很大。
规约很多时候都是指“多项式规约”。
(这部分不太确定)
NP-完全问题和 NP-难问题 NP-完全问题 (NPC, NP-Complete) 必须同时满足:
L ∈ N P L \in \mathbf{NP} L ∈ NP ∀ L ′ ∈ N P \forall L' \in \mathbf{NP} ∀ L ′ ∈ NP L ′ ≤ p L L' \leq_p L L ′ ≤ p L 即:L L L
证明一个问题是 NP-完全问题 证明该问题 L ∈ N P L \in \mathbf{NP} L ∈ NP 从某个已知的 NP-完全问题(如 SAT、3-SAT、CLIQUE、SUBSET SUM 等)出发; 构造一个多项式时间归约 :将已知问题的任意实例转化为当前问题的实例; 说明:如果新问题可解,则原问题也可解 ,从而说明当前问题至少和已知问题一样难。 NP-难问题 (NP-Hard) 满足 ∀ L ′ ∈ N P \forall L' \in \mathbf{NP} ∀ L ′ ∈ NP L ′ ≤ p L L' \leq_p L L ′ ≤ p L L ∈ N P L \in \mathbf{NP} L ∈ NP
N P C ⊆ N P − H a r d \mathbf{NPC} \subseteq \mathbf{NP-Hard} NPC ⊆ NP − Hard
SAT 问题 SAT 问题 (布尔可满足性问题 ,又叫可满足性问题 ),即给定布尔公式(合取范式 CNF, Conjunctive Normal Form),判断是否存在一种赋值使公式为真。
F = C 1 ∧ C 2 ∧ ⋯ ∧ C k F = C_1 \land C_2 \land \cdots \land C_k F = C 1 ∧ C 2 ∧ ⋯ ∧ C k
其中每个子句 C j C_j C j C j = ( σ 1 ∨ σ 2 ∨ ⋯ ) C_j = (\sigma_1 \lor \sigma_2 \lor \cdots) C j = ( σ 1 ∨ σ 2 ∨ ⋯ )
例如:
F 1 = ( x 1 ∨ x 2 ) ∧ ( ¬ x 1 ∨ x 2 ∨ x 3 ) ∧ ¬ x 2 F_1 = (x_1 \lor x_2) \land (\lnot x_1 \lor x_2 \lor x_3) \land \lnot x_2 F 1 = ( x 1 ∨ x 2 ) ∧ ( ¬ x 1 ∨ x 2 ∨ x 3 ) ∧ ¬ x 2 ( 1 , 0 , 1 ) (1,0,1) ( 1 , 0 , 1 ) F 2 = ( x 1 ∧ ¬ x 2 ∧ x 3 ) ∧ ( ¬ x 1 ∨ ¬ x 2 ∨ x 3 ) ∧ x 2 ∧ ¬ x 3 F_2 = (x_1 \land \lnot x_2 \land x_3) \land (\lnot x_1 \lor \lnot x_2 \lor x_3) \land x_2 \land \lnot x_3 F 2 = ( x 1 ∧ ¬ x 2 ∧ x 3 ) ∧ ( ¬ x 1 ∨ ¬ x 2 ∨ x 3 ) ∧ x 2 ∧ ¬ x 3 Cook定理 :
任何 NP-问题都可以归约为 SAT 问题,即:
∀ L ∈ N P , ∃ T : L ≤ p SAT \forall L \in \mathbf{NP}, \exists T: L \leq_p \text{SAT} ∀ L ∈ NP , ∃ T : L ≤ p SAT
常见的 NP-完全问题 恰好覆盖问题 :
给定集合 A = { a 1 , a 2 , … , a n } A = \{a_1, a_2, \dots, a_n\} A = { a 1 , a 2 , … , a n } W = { S 1 , S 2 , … , S m } W = \{S_1, S_2, \dots, S_m\} W = { S 1 , S 2 , … , S m } U ⊆ W U \subseteq W U ⊆ W
所有 S ∈ U S \in U S ∈ U 互不相交 并集等于 A A A 子集和问题 :
给定整数集合 X = { x 1 , x 2 , … , x n } X = \{x_1, x_2, \dots, x_n\} X = { x 1 , x 2 , … , x n } N N N T ⊆ X T \subseteq X T ⊆ X
∑ x ∈ T x = N \sum_{x \in T} x = N x ∈ T ∑ x = N
可通过下面的归约证明:
Exact Cover ≤ p Subset Sum \text{Exact Cover} \leq_p \text{Subset Sum} Exact Cover ≤ p Subset Sum
旅行商问题的判定问题 :
给定一组城市及城市之间的距离,以及一个距离上限 K K K K K K
要验证给定的一条路径是否合法、且总距离是否小于等于 K K K
另外,它可以规约为一个哈密顿回路问题,而后者是一个 NPC 问题。
参考和注解